Question

（1）问题探究
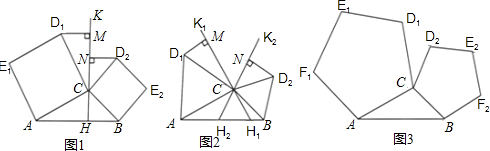
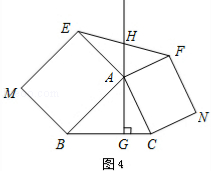
如图1，分别以△ABC的边AC与边BC为边，向△ABC外作正方形ACD₁E₁和正方形BCD₂E₂，过点C
作直线KH交直线AB于点H，使∠AHK=∠ACD₁作D₁M⊥KH，D₂N⊥KH，垂足分别为点M，N．试探究线段D₁M与线段D₂N的数量关系，并加以证明．
（2）拓展延伸
①如图2，若将“问题探究”中的正方形改为正三角形，过点C作直线K₁H₁，K₂H₂，分别交直线AB于点H₁，H₂，使∠AH₁K₁=∠BH₂K₂=∠ACD₁．作D₁M⊥K₁H₁，D₂N⊥K₂H₂，垂足分别为点M，N．D₁M=D₂N是否仍成立？若成立，给出证明；若不成立，说明理由．
②如图3，若将①中的“正三角形”改为“正五边形”，其他条件不变．D₁M=D₂N是否仍成立？（要求：在
图3中补全图形，注明字母，直接写出结论，不需证明）

Answer 1

解：（1）D₁M=D₂N。证明如下：
∵∠ACD₁=90°，∴∠ACH+∠D₁CK=180°﹣90°=90°。
∵∠AHK=∠ACD₁=90°，∴∠ACH+∠HAC=90°。
∴∠D₁CK=∠HAC。
在△ACH和△CD₁M中，∠D₁CK=∠HAC，∠AHC="∠C" M D₁=90°，AC="C" D₁，
∴△ACH≌△CD₁M（AAS）。∴D₁M=CH。
同理可证D₂N=CH。
∴D₁M=D₂N。
（2）①D₁M=D₂N成立。证明如下：
过点C作CG⊥AB，垂足为点G，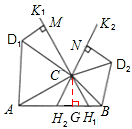

∵∠H₁AC+∠ACH₁+∠AH₁C=180°，
∠D₁CM+∠ACH₁+∠ACD₁=180°，∠AH₁C=∠ACD₁，
∴∠H₁AC=∠D₁CM。
在△ACG和△CD₁M中，∠H₁AC=∠D₁CM，∠AGC="∠C" M D₁=90°，AC="C" D₁，
∴△ACG≌△CD₁M（AAS）。∴CG=D₁M。
同理可证CG=D₂N。
∴D₁M=D₂N。
②作图如下：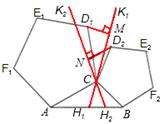

D₁M=D₂N还成立。

解析