Question

（1）操作发现：
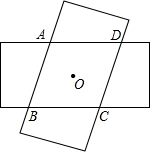
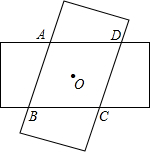
如图，有两条长9cm，宽3cm的矩形重合后绕中心O旋转的到ABCD，试判断四边形ABCD是什么特殊四边形？并说明理由．
（2）尝试探索：
在旋转过程中，四边形ABCD的最小面积是________cm²，
在旋转过程中，四边形ABCD的最大面积是多少？画图计算．

Answer 1

解：（1）重叠四边形ABCD是菱形．理由如下：
根据矩形对边平行，可得ABCD是平行四边形；
因为矩形等宽，即ABCD各边上的高相等．
根据平行四边形的面积公式可得邻边相等，
所以ABCD是菱形．

（2）当菱形ABCD为正方形时，s_最小=3²=9（cm²）；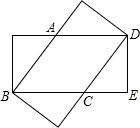
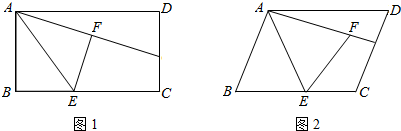
当菱形ABCD如图时，面积最大．
设CD=x，根据勾股定理得x²=（9-x）²+3²，
解得x=5．
∴s_最大=BC×DE=5×3=15（cm²）．
分析：（1）易证ABCD为平行四边形；根据矩形等宽，说明平行四边形的各边上的高相等，利用等积表示法证明邻边相等．根据有一组邻边相等的平行四边形是菱形得证；
（2）当ABCD为正方形时面积最小；当对角线重合时的菱形面积最大．分别计算求解．
点评：此题考查了旋转的性质、矩形的性质、菱形的判定方法及面积的计算问题．应明白在什么情况下重叠面积最小或最大，这是此题的难点．