题目内容
童话故事:“龟兔赛跑”:兔子和乌龟同时从起点出发,比赛跑步.领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边的小树下睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟已先到达终点.
数学探究:
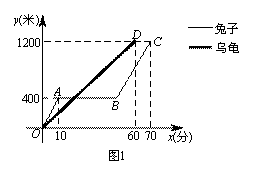
我们假设乌龟、兔子的速度及赛场均保持不变.小莉用图①刻画了“龟兔赛跑”的故事,
其中x(分)表示乌龟从起点出发所行的时间,y1(米)表示兔子所行的路程,y2(米)表示乌龟所行的路程.
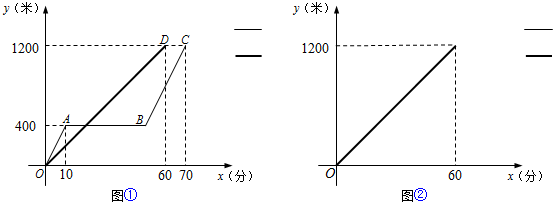
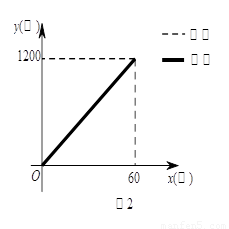
(1)分别求线段BC、OD所表示的y1、y2与x之间的函数关系式;
(2)试解释图中线段AB的实际意义;
(3)兔子输了比赛,心里很不服气,它们约定再次赛跑.
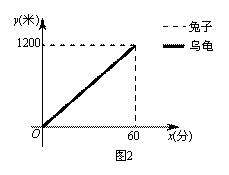
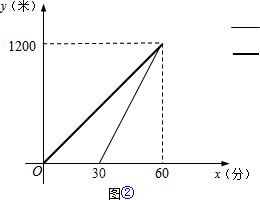
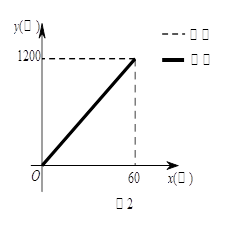
①如果兔子让乌龟先跑30分钟,它才开始追 赶.请在图②中画出兔子所行的路程y1与x之间的函数关系的图象,并直接判断谁先到达终点;
②如果兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,它们同时出发,这一次谁先到达终点呢?为什么?
解:(1)由图知,兔子的速度为:400÷10=40(米/分),
所以点B的横坐标为:70-(1200-400)÷40=50,
设线段BC所表示的函数关系式为y1=kx+b,
则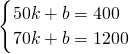 ,
,
解得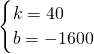 ,
,
所以,线段BC所表示的函数关系式为y1=40x-1600,其中50≤x≤70,
线段OD所表示的函数关系式为y2=20x,
其中0≤x≤60;
(2)出发10分后,兔子在路边的小树下睡了40分,
小树距起点400米;
(3)兔子到达终点所需时间为:1200÷40=30(分),
如图②,同时到达终点;
(4)兔子所需时间:1200÷40=30(分),
乌龟所需时间:800÷20=40(分),
所以兔子先到终点.
分析:(1)先求出兔子的速度,然后求出点B的横坐标,再设线段BC的解析式为y1=kx+b,利用待定系数法求一次函数解析式求出y1,再利用待定系数法求出y2的解析式;
(2)根据AB的函数值没有发生变化可知兔子在睡觉;
(3)①根据时间=路程÷速度求出兔子到达终点的时间,然后作出图象即可得解;
②根据时间=路程÷速度分别求出兔子与乌龟到达终点的时间,即可判断.
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,时间、速度、路程三者之间的关系,读懂题目信息,理清数量关系是解题的关键.
所以点B的横坐标为:70-(1200-400)÷40=50,
设线段BC所表示的函数关系式为y1=kx+b,
则
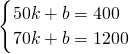 ,
,解得
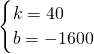 ,
,所以,线段BC所表示的函数关系式为y1=40x-1600,其中50≤x≤70,
线段OD所表示的函数关系式为y2=20x,
其中0≤x≤60;

(2)出发10分后,兔子在路边的小树下睡了40分,
小树距起点400米;
(3)兔子到达终点所需时间为:1200÷40=30(分),
如图②,同时到达终点;
(4)兔子所需时间:1200÷40=30(分),
乌龟所需时间:800÷20=40(分),
所以兔子先到终点.
分析:(1)先求出兔子的速度,然后求出点B的横坐标,再设线段BC的解析式为y1=kx+b,利用待定系数法求一次函数解析式求出y1,再利用待定系数法求出y2的解析式;
(2)根据AB的函数值没有发生变化可知兔子在睡觉;
(3)①根据时间=路程÷速度求出兔子到达终点的时间,然后作出图象即可得解;
②根据时间=路程÷速度分别求出兔子与乌龟到达终点的时间,即可判断.
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,时间、速度、路程三者之间的关系,读懂题目信息,理清数量关系是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
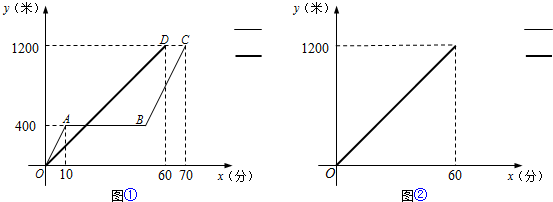
 (分)表示乌龟从起点出发所行的时间,
(分)表示乌龟从起点出发所行的时间,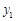 (米)表示兔子所行的路程,
(米)表示兔子所行的路程,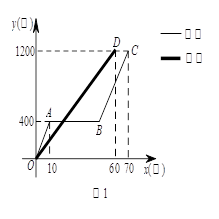
 、
、 所表示的
所表示的 与
与 的实际意义;
的实际意义;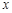 (分)表示乌龟从起点出发所行的时间,
(分)表示乌龟从起点出发所行的时间,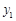 (米)表示兔子所行的路程,
(米)表示兔子所行的路程,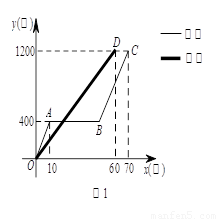
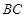 、
、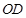 所表示的
所表示的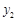 与
与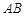 的实际意义;
的实际意义;