Question

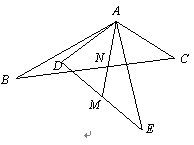
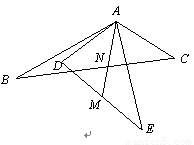
 （本题10分）如右图，点A是△ABC和△ADE的公共顶点，∠BAC＋∠DAE＝180°，AB＝AE，AC＝AD，点M是DE的中点，直线AM交直线BC于点N．将△ADE绕点A旋转，在旋转的过程中，请探究∠ANB与∠BAE的数量关系，并加以证明.

 

Answer 1

【答案】

 

②当点N为射线AM的反向延长线与射线BC的反向延长线的交点时，如图3，∠ANB与∠BAE互补，即∠ANB+∠BAE=180º．

证明： 同①可得∠ABC=∠EAF，∴∠ABN=∠EAN（等角的补角相等），

又∵△ ANB中，∠ANB+∠ABN+∠BAN=180º，

∴∠ANB+∠EAN +∠BAN =180º，即∠ANB+∠BAE=180º．      ……（7分）

 

③当点N为射线AM的反向延长线与射线BC的交点时，如图4、图5.∠ANB=∠BAE.证明：同①可得∠ABC=∠EAF，

又∵∠BAF=∠ABC+∠ANB，∠BAF =∠EAF +∠BAE，∴∠ANB=∠BAE． ……（9分）                                  

④当点N为射线AM 与射线BC的反向延长线的交点时，如图6.∠ANB=∠BAE.

证明：同①可得∠ABC=∠EAF，

∵∠ABC=∠ANB+∠NAB，∠EAF=∠BAE+∠NAB，∴∠ANB=∠BAE．  ……（10分）

【解析】略