题目内容
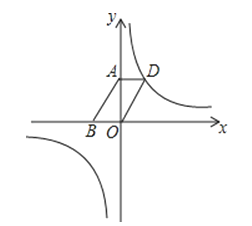
【题目】如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30方向12km处,位于景点B的正北方向,还位于景点C的北偏西75方向上.已知AB=![]() km.
km.
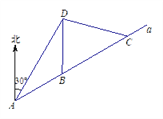
(1)现准备由景点D向公路a修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;
(2)求出景点B与景点C之间的距离(结果保留根号).
【答案】(1)6km;(2)![]() .
.
【解析】试题分析:(1) 过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,求DE的问题就可以转化为求∠DBE的度数或三角函数值的问题;(2)Rt△DCE中根据三角函数就可以求出CD的长.
试题解析: (1)如图,过点D作DE⊥AC于点E,

过点A作AF⊥DB,交DB的延长线于点F,
在Rt△DAF中,∠ADF=30°,
∴AF=![]() AD=
AD=![]() ×12=6,
×12=6,
∴DF=![]() =
=![]() =6
=6![]() ,
,
在Rt△ABF中BF=![]() =
=![]() =2
=2![]() ,
,
∴BD=DFBF=6![]() -2
-2![]() =4
=4![]() ,
,
sin∠ABF=![]() =
=![]() ,
,
在Rt△DBE中,sin∠DBE=![]() ,
,
∵∠ABF=∠DBE,
∴sin∠DBE=![]() ,
,
∴DE=BDsin∠DBE=![]() ×4
×4![]() =6(km),
=6(km),
∴景点D向公路a修建的这条公路的长约是6km;
(2)由题意可知∠CDB=75°,
由(1)可知sin∠DBE=![]() ,所以∠DBE=60°,
,所以∠DBE=60°,
∴∠DCB=180°75°60°=45°,
在Rt△DCE中,CE=DE=6 (km),
在Rt△DBE中, ∠BDE=75°-45°=30°,
∴BE=![]() BD=
BD=![]() (km),
(km),
∴BC=6+![]() (km)
(km)
∴景点B与景点C之间的距离为6+![]() km.
km.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】甲、乙、丙、丁四人参加射击训练,每人各射击20次,他们射击成绩的平均数都是9.1环,各自的方差见如下表格:
甲 | 乙 | 丙 | 丁 | |
方差 | 0.293 | 0.375 | 0.362 | 0.398 |
由上可知射击成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁