题目内容
(2009•宝山区一模)已知抛物线y=x2-(m+1)x+m与y轴交于点P(0,-3),则m= .
【答案】分析:把点P(0,-3)代入y=x2-(m+1)x+m,即可求出m的值.
解答:解:∵抛物线y=x2-(m+1)x+m与y轴交于点P(0,-3),
∴-3=m,
∴m=-3.
点评:本题考查了函数图象上的点的坐标与函数解析式的关系.
解答:解:∵抛物线y=x2-(m+1)x+m与y轴交于点P(0,-3),
∴-3=m,
∴m=-3.
点评:本题考查了函数图象上的点的坐标与函数解析式的关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
(2009•宝山区一模)“三聚氰胺事件”对奶制品行业影响很大.为应对该事件对行业的冲击,某品牌奶糖生产企业研制出甲、乙两种新配方奶糖,已试销近三个月、已知这两种奶糖的成本价相同,售价也相同(售价不低于成本价)、为了解销售情况,营销人员进行了市场调查,并对某区域的销售数据进行了分析,发现甲、乙两种配方奶糖的日销量Q甲、Q乙(千克)与它们的售价x(元/千克)之间均具有一次函数关系,部分数据见右表.又知当售价为25元时,甲种配方奶糖的日销售利润为450元.[注:日销售利润=(销售价-成本价)×日销售量.]
(1)根据上述信息,研究人员求出Q乙=-2x+135.请你求出Q甲关于x的函数解析式,并写出定义域;
(2)求甲种配方奶糖的日销售利润W乙(元)关于x的函数解析式;
(3)根据上述信息,试分析当售价为多少元时,该区域甲、乙两种配方奶糖的日销售利润之和最大,并求出最大值.
| X | …. | 25 | 30 | …. |
| Q甲 | …. | 90 | 75 | …. |
| Q乙 | …. | 85 | 75 | … |
(2)求甲种配方奶糖的日销售利润W乙(元)关于x的函数解析式;
(3)根据上述信息,试分析当售价为多少元时,该区域甲、乙两种配方奶糖的日销售利润之和最大,并求出最大值.
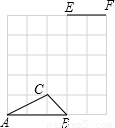
 三点.
三点.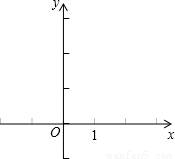
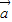 、
、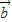 ,且
,且 .
.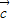 ;
; ,试说明
,试说明 ∥
∥ .
.