题目内容
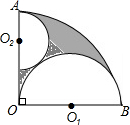 如图,扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切.
如图,扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切.(1)求半圆O1与半圆O2的半径比;
(2)若OB=12,求图中阴影部分的面积.
分析:(1)根据两圆外切两圆连心线必过圆心,进而利用勾股定理得出两圆半径的关系;
(2)利用(1)中所求,进而得出两圆的半径,再利用扇形面积求出即可.
(2)利用(1)中所求,进而得出两圆的半径,再利用扇形面积求出即可.
解答:解:(1)连接O1O2,设半圆O1与半圆O2的半径分别为:x,y,
∵扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切,
∴OO1=x,OO2=2x-y,O1O2=x+y,
∴x2+(2x-y)2=(x+y)2,
整理得出:4x=6y,
∴
=
=
;
(2)∵OB=12,
∴O1B=6,AO2=4,
∴图中阴影部分的面积为:S扇形AOB-S半圆O2-S半圆O1=
-
-
=10π.
∵扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切,
∴OO1=x,OO2=2x-y,O1O2=x+y,
∴x2+(2x-y)2=(x+y)2,
整理得出:4x=6y,
∴
| x |
| y |
| 6 |
| 4 |
| 3 |
| 2 |
(2)∵OB=12,
∴O1B=6,AO2=4,
∴图中阴影部分的面积为:S扇形AOB-S半圆O2-S半圆O1=
| 90π×122 |
| 360 |
| π×42 |
| 2 |
| π×62 |
| 2 |
点评:此题主要考查了相切两圆的性质和扇形面积公式应用,得出两圆的半径是解题关键.

练习册系列答案
相关题目
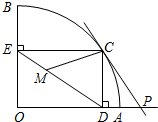 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
 (2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,

