题目内容
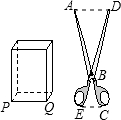如图，有一把剪刀，AB=2BC，DB=2BE，剪刀前面有一长方体，宽PQ=12cm，想用剪刀的A、D两点夹住P、Q两点，那么手握的地方CE至少要张开多少？
解：∵AB=2BC，DB=2BE，
∴
，
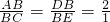∵∠ABD=∠CBE，
∴△ABC∽△ACD，
∴
，
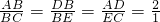当AD=PQ=12时，CE=6cm．
分析：首先利用对应边的比相等且夹角相等求得△ABC∽△ACD，然后利用相似三角形对应边的比相等求得线段CE的长即可．
点评：本题考查了相似三角形的应用，从实际问题中整理出相似三角形是解决本题的关键．
∴
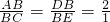，∵∠ABD=∠CBE，
∴△ABC∽△ACD，
∴
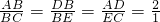，当AD=PQ=12时，CE=6cm．
分析：首先利用对应边的比相等且夹角相等求得△ABC∽△ACD，然后利用相似三角形对应边的比相等求得线段CE的长即可．
点评：本题考查了相似三角形的应用，从实际问题中整理出相似三角形是解决本题的关键．
练习册系列答案
相关题目
10、如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是（ ）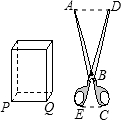
如图，有一把剪刀，AB=2BC，DB=2BE，剪刀前面有一长方体，宽PQ=12cm，想用剪刀的A、D两点夹住P、Q两点，那么手握的地方CE至少要张开多少？
