题目内容
(2002•昆明)如图,正六边形ABCDEF中,阴影部分面积为12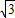 cm2,则此正六边形的边长为( )
cm2,则此正六边形的边长为( )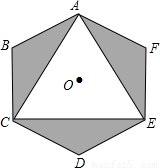
A.2cm
B.4cm
C.6cm
D.8cm
【答案】分析:阴影部分的面积是正六边形的面积与正三角形面积的差,这两个正多边形有共同的半径,可以设半径是R,根据阴影部分面积为12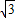 cm2,就可得到关于R的方程,从而解得R的值.
cm2,就可得到关于R的方程,从而解得R的值.
解答:解:由正六边形可分成六个全等的等边三角形,正六边形的中心角和内角都是120°.
则阴影部分的面积与中间的正三角形的面积相等,即阴影部分的面积为正六边形的面积的一半.
设边长为R,
所以有6× ×R2×sin60°=2×2
×R2×sin60°=2×2 ,
,
∴R=4cm.
故选B.
点评:本题考查了正六边形的性质,明白阴影部分的面积是正六边形的面积的一半是解题的关键.
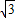 cm2,就可得到关于R的方程,从而解得R的值.
cm2,就可得到关于R的方程,从而解得R的值.解答:解:由正六边形可分成六个全等的等边三角形,正六边形的中心角和内角都是120°.
则阴影部分的面积与中间的正三角形的面积相等,即阴影部分的面积为正六边形的面积的一半.
设边长为R,
所以有6×
 ×R2×sin60°=2×2
×R2×sin60°=2×2 ,
,∴R=4cm.
故选B.
点评:本题考查了正六边形的性质,明白阴影部分的面积是正六边形的面积的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上一动点,当点A的位置在 时,△ABE∽△ACB.
上一动点,当点A的位置在 时,△ABE∽△ACB.

 上一动点,当点A的位置在 时,△ABE∽△ACB.
上一动点,当点A的位置在 时,△ABE∽△ACB.