题目内容
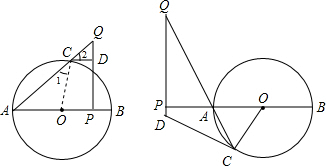
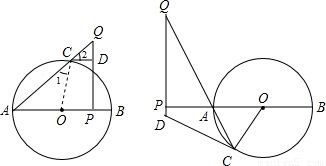
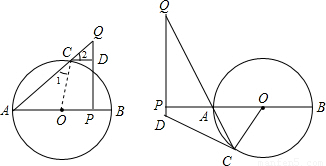
如图，在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′．（1）在坐标纸上画出这几次变换相应的图形；
（2）设P（x，y）为△OAB边上任一点，依次写出这几次变换后点P对应点的坐标．
【答案】分析：分别根据位似变换、轴对称、平移的作图方法作图即可；根据这些变换的特点可求出变换后点P对应点的坐标．
解答：
解：（1）如图．先把△ABC作位似变换，扩大2倍，再作关于y轴对称的三角形，然后向右平移4个单位，再向上平移5个单位．
（2）设坐标纸中方格边长为单位1，则P（x，y）以O为位似中心放大为原来的2倍（2x，2y），经y轴翻折得到（-2x，2y），再向右平移4个单位得到（-2x+4，2y），再向上平移5个单位得到（-2x+4，2y+5）．
点评：本题主要考查：位似变换、轴对称、平移．此题隐含着逆向思维．
解答：
解：（1）如图．先把△ABC作位似变换，扩大2倍，再作关于y轴对称的三角形，然后向右平移4个单位，再向上平移5个单位．（2）设坐标纸中方格边长为单位1，则P（x，y）以O为位似中心放大为原来的2倍（2x，2y），经y轴翻折得到（-2x，2y），再向右平移4个单位得到（-2x+4，2y），再向上平移5个单位得到（-2x+4，2y+5）．
点评：本题主要考查：位似变换、轴对称、平移．此题隐含着逆向思维．
练习册系列答案
相关题目
