题目内容
(1999•贵阳)下列命题中错误的有( )(1)相切两圆的连心线经过切点;(2)平分弦的直径垂直于弦;(3)梯形的对角线互相平分;(4)圆的对称轴是直径.A.1个
B.2个
C.3个
D.4个
【答案】分析:根据圆中的定理进行分析.
相切两圆的性质:相切两圆的连心线经过切点;
垂径定理的推论:平分弦(非直径)的直径垂直于弦.
解答:解:(1)根据相切两圆的性质,故正确;
(2)根据垂径定理的推论,则当该弦是直径时,不一定垂直,故错误;
(3)若对角线互相平分,则一定是平行四边形,故错误;
(4)对称轴应是直线,即圆的对称轴是直径所在的直线,故错误.
故选C.
点评:熟悉圆中的定理.
相切两圆的性质:相切两圆的连心线经过切点;
垂径定理的推论:平分弦(非直径)的直径垂直于弦.
解答:解:(1)根据相切两圆的性质,故正确;
(2)根据垂径定理的推论,则当该弦是直径时,不一定垂直,故错误;
(3)若对角线互相平分,则一定是平行四边形,故错误;
(4)对称轴应是直线,即圆的对称轴是直径所在的直线,故错误.
故选C.
点评:熟悉圆中的定理.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
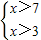 的解集是x>3
的解集是x>3 的解集是-3<x<-2
的解集是-3<x<-2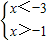 的解集是x<-1
的解集是x<-1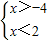 的解集是-4<x<2
的解集是-4<x<2