题目内容
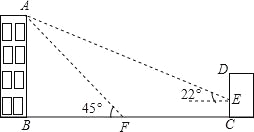
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
【答案】(1)12;
(2)27
【解析】
试题分析:(1)首先构造直角三角形△AEM,利用tan22°=![]() ,求出即可;
,求出即可;
(2)利用Rt△AME中,cos22°=![]() ,求出AE即可.
,求出AE即可.
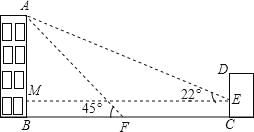
试题解析:(1)过点E作EM⊥AB,垂足为M.设AB为x.
Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,
tan22°=![]() ,则
,则![]() =
=![]() ,解得:x=12.即教学楼的高12m.
,解得:x=12.即教学楼的高12m.
(2)由(1)可得ME=BC=x+13=12+13=25.在Rt△AME中,cos22°=![]() .∴AE=
.∴AE=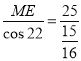 ≈27,
≈27,
即A、E之间的距离约为27m.

练习册系列答案
相关题目
【题目】二中对初三男生进行了引体向上的测试,以能做七个为标准,超过的次数用正数表示,不足的次数用负数表示,其中8名男生的成绩如下表:
2 | -1 | 0 | 3 | -2 | -3 | 1 | 0 |
(1)这8名男生有百分之几达到标准?
(2)他们共做了多少各引体向上?