题目内容
如图，AC⊥CE于C，AD=BE=13，点B、D分别在AC、EC上，且BC=5，DE=7，则AC=
12
12
．分析：首先，在直角△BEC中，利用勾股定理求得BC=12，所以DC=EC-DE=12-7=5．在直角△ADC中，∠C=90°，AD=13，CD=5，则由勾股定理得到：AC=
=12．
| AD2-DC2 |
解答：解：如图，∵在直角△BEC中，∠C=90°，BE=13，BC=5，
∴由勾股定理得到：EC=
=
=12．
∵DE=7，
∴DC=EC-DE=12-7=5．
∴在直角△ADC中，∠C=90°，AD=13，CD=5，
∴由勾股定理得到：AC=
=
=12．
故填：12．
∴由勾股定理得到：EC=
| BE2-BC2 |
| 132-52 |
∵DE=7，
∴DC=EC-DE=12-7=5．
∴在直角△ADC中，∠C=90°，AD=13，CD=5，
∴由勾股定理得到：AC=
| AD2-DC2 |
| 132-52 |
故填：12．
点评：本题考查了勾股定理．勾股定理应用的前提条件是在直角三角形中．
练习册系列答案
相关题目
22、如图：AC⊥CE于C，DE⊥CE于E，∠1=40°．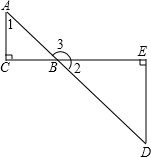
如图：AC⊥CE于C，DE⊥CE于E，∠1=40°．
