题目内容
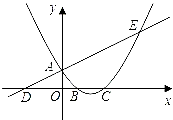
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线交于
与直线交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() 点坐标为(1,0).
点坐标为(1,0).
(1)求该抛物线的解析式;
(2)动点![]() 在
在![]() 轴上移动,当△
轴上移动,当△![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点![]() ,使|
,使|![]() |的值最大,求出点
|的值最大,求出点![]() 的坐标.
的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+1;(2)(
x+1;(2)(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0);(3)M(1.5,-0.5)
,0);(3)M(1.5,-0.5)
【解析】
试题分析:(1)首先根据直线解析式求出点A、B的坐标,然后代入二次函数解析式得出解析式;(2)根据直角三角形的性质得出点P的坐标;(3)首先得出抛物线的对称轴,则MC=MB,要使|AM﹣MC|最大,即是使|AM﹣MB|最大,由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大,求出直线AB的解析式,直线AB与对称轴的交点就是点M.
试题解析:(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() 得A(0,1),
得A(0,1),
将A(0,1)、B(1,0)坐标代入y=![]() x2+bx+c
x2+bx+c
得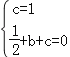 ,
,
解得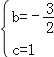 ,
,
∴抛物线的解折式为y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)满足条件的点P的坐标为(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0)
,0)
(3)抛物线的对称轴为![]()
∵B、C关于x=![]() 对称,
对称,
∴MC=MB,
要使|AM﹣MC|最大,即是使|AM﹣MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大.
易知直线AB的解折式为y=﹣x+1
∴由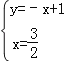 ,得
,得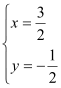
∴M(1.5,-0.5)

练习册系列答案
相关题目