题目内容
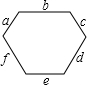如图，一个凸六边形的六个内角都是120°，六条边的长分别为a，b，c，d，e，f，则下列等式中成立的是
- A.a+b+c=d+e+f
- B.a+c+e=b+d+f
- C.a+b=d+e
- D.a+c=b+d
C
分析：如解答中图，连接AB，过E作EC∥AG，过F作FD∥AH，易得三角形BCE和BDF是等边三角形，四边形ACEG和ADFH是平行四边形．可得AB=b+c=d+e，a=c，d=f．
解答：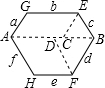
解：如图，连接AB，过E作EC∥AG，过F作FD∥AH，
∵六个内角都是120°显然GE∥HF，
∴四边形ACEG和ADFH是平行四边形，三角形BCE和BDF是等边三角形，四边形ABEG和ABFH是等腰梯形
∴AB=b+c=d+e，a=c，d=f．
可知a+b=d+e．
故选C．
点评：考查了平行四边形与等边三角形的性质及其应用．
分析：如解答中图，连接AB，过E作EC∥AG，过F作FD∥AH，易得三角形BCE和BDF是等边三角形，四边形ACEG和ADFH是平行四边形．可得AB=b+c=d+e，a=c，d=f．
解答：
解：如图，连接AB，过E作EC∥AG，过F作FD∥AH，∵六个内角都是120°显然GE∥HF，
∴四边形ACEG和ADFH是平行四边形，三角形BCE和BDF是等边三角形，四边形ABEG和ABFH是等腰梯形
∴AB=b+c=d+e，a=c，d=f．
可知a+b=d+e．
故选C．
点评：考查了平行四边形与等边三角形的性质及其应用．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
25、如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架的稳定性、对称性、实用性等因素，请再加三根竹条与其顶点连接．
54、如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架的稳固性、美观性、实用性等因素，需再加竹条与其顶点连接．要求：
7、如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架的稳定性、对称性、实用性等因素，请再加三根竹条与其顶点连接，设计出两种不同的连接方案（用直尺连接）．
