题目内容
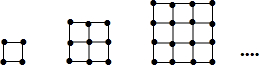
如图,用火柴棒摆成边长为1,2,3,…,(n-1),n的正方形

(1)依此规律,摆成边长为4的正方形图案中,需火柴棒根数为________;
(2)拼成边长为n的正方形图案比边长为(n-1)的正方形图案多________个小正方形;
(3)摆成边长为n的正方形图案中需要火柴棒根数为________.
解:当边长为1根火柴棍时,设摆出的正方形所用的火柴棍的根数为4=2×1×(1+1);
当边长为2根火柴棍时,设摆出的正方形所用的火柴棍的根数为12=2×2×(2+1);
当边长为3根火柴棍时,设摆出的正方形所用的火柴棍的根数为24=2×3×(3+1);
…;
故当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为2n(n+1).
(1)当摆成的边长为4的正方形图案,需要火柴2×4×(4+1)=40;
(2)根据题意得:2n(n+1)-2(n-1)n=2n-1;
(3)摆成边长为n的正方形图案中需要火柴棒根数为2n(n+1).
故答案为:(1)40;(2)2n-1;(3)2n(n+1).
分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
点评:此题考查的知识点是图形数字的变化类问题,关键是通过摆出火柴棍的根数找出规律,按规律求解.
当边长为2根火柴棍时,设摆出的正方形所用的火柴棍的根数为12=2×2×(2+1);
当边长为3根火柴棍时,设摆出的正方形所用的火柴棍的根数为24=2×3×(3+1);
…;
故当边长为n根火柴棍时,设摆出的正方形所用的火柴棍的根数为2n(n+1).
(1)当摆成的边长为4的正方形图案,需要火柴2×4×(4+1)=40;
(2)根据题意得:2n(n+1)-2(n-1)n=2n-1;
(3)摆成边长为n的正方形图案中需要火柴棒根数为2n(n+1).
故答案为:(1)40;(2)2n-1;(3)2n(n+1).
分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
点评:此题考查的知识点是图形数字的变化类问题,关键是通过摆出火柴棍的根数找出规律,按规律求解.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
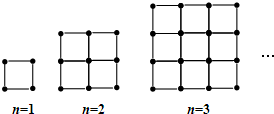 如图所示,用火柴棒摆成边长分别是1、2、3、…根火柴棒时的正方形,当边长为60根火柴棒时,若摆出的正方形所用的火柴棒的根数为S,则S=
如图所示,用火柴棒摆成边长分别是1、2、3、…根火柴棒时的正方形,当边长为60根火柴棒时,若摆出的正方形所用的火柴棒的根数为S,则S=