题目内容
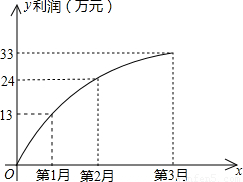
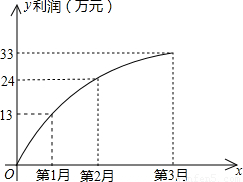
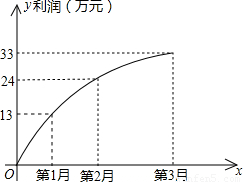
(2008•乐山)一家电脑公司推出一款新型电脑,投放市场以来的利润情况可以看做是抛物线的一部分,请结合下面的图象解答以下问题:(1)求该抛物线对应的二次函数的解析式;
(2)该公司在经营此款电脑过程中,第几个月的利润最大,最大利润是多少;
(3)若照此经营下去,请你结合所学的知识,对公司在此款电脑的经营状况(是否亏损何时亏损)作出预测.
【答案】分析:要根据抛物线在坐标系的位置合理性质抛物线解析式的形式,因为图象过原点,故可设该二次函数的解析式为:y=ax2+bx,根据图形中的已知两点确定解析式,运用二次函数的性质解题.
解答:解:(1)因为图象过原点,故可设该二次函数的解析式为:y=ax2+bx
由图知,图象过(1,13),(2,24)点,代入解析式得: ,
,
解得: ,
,
∴y=-x2+14x.
(2)∵y=-x2+14x=-(x-7)2+49
∴当x= =7时,利润最大
=7时,利润最大
最大值为y=0+49=49(万元)
该公司在经营此款电脑时,第7个月的利润最大,最大利润是49万元.
(3)当y=0,-x2+14x=0,解得:
x=14或x=0(舍去)
故从第15个月起,公司将出现亏损.
点评:从纵向上看,抛物线的最高点就是函数的最大值,即最大利润;从横向上看,当抛物线与x轴相交时,利润为0,图象在x轴下方,就出现亏损.
解答:解:(1)因为图象过原点,故可设该二次函数的解析式为:y=ax2+bx
由图知,图象过(1,13),(2,24)点,代入解析式得:
 ,
,解得:
 ,
,∴y=-x2+14x.
(2)∵y=-x2+14x=-(x-7)2+49
∴当x=
 =7时,利润最大
=7时,利润最大最大值为y=0+49=49(万元)
该公司在经营此款电脑时,第7个月的利润最大,最大利润是49万元.
(3)当y=0,-x2+14x=0,解得:
x=14或x=0(舍去)
故从第15个月起,公司将出现亏损.
点评:从纵向上看,抛物线的最高点就是函数的最大值,即最大利润;从横向上看,当抛物线与x轴相交时,利润为0,图象在x轴下方,就出现亏损.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ;
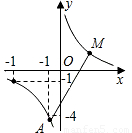
;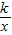 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.
 的是否为定值?若是,求出该定值;若不是,请说明理由.
的是否为定值?若是,求出该定值;若不是,请说明理由.