题目内容
【题目】如图,在△ABC中,∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
【答案】证明:连接PA, 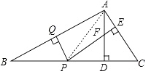
则PA=PB,
∴∠B=∠PAB=22.5° ,
∴∠APD=45°.
又∵AD⊥BC
∴PD=AD.
∵AD⊥BC,
∴∠DPF+∠PFD=90°.
∵PE⊥AC,
∴∠AFE+∠DAC=90°.
又∵∠AFE=∠PFD,
∴∠DPF=∠DAC.
在△PDF和△ADC中, 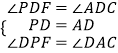
∴△PDF≌△ADC(ASA).
∴DF=DC.
【解析】:连接PA,根据中垂线的性质定理得出PA=PB,根据等边对等角得出∠B=∠PAB=22.5° ,根据三角形的外角定理得出∠APD=45°,根据等腰直角三角形的性质得出PD=AD ,然后根据等角的余角相等得出∠DPF=∠DAC,然后利用ASA判断出△PDF≌△ADC ,根据全等三角形对应边相等得出DF=DC.
【考点精析】利用余角和补角的特征和三角形的外角对题目进行判断即可得到答案,需要熟知互余、互补是指两个角的数量关系,与两个角的位置无关;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目