题目内容
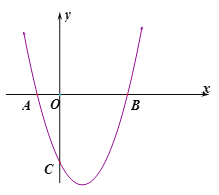
【题目】如图，二次函数y＝﹣x2+3x+m的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．
（1）求m的值及C点坐标；
（2）在抛物线的对称轴上是否存在一点M，使得它到B、C两点的距离和最小，若存在，求出此时M点坐标，若不存在，请说明理由；
（3）P为抛物线上一点，它关于直线BC的对称点为Q，当四边形PBQC为菱形时，请直接写出点P的坐标．
【答案】（1）m=4，C（0，4）；（2）存在M（
），见解析；（3）P（
）或P（
）.
【解析】
（1）用待定系数法求出抛物线解析式；
（2）先求得点C的坐标，然后依据待定系数法求得直线BC的解析式，然后再求得抛物线的对称轴方程，由三角形的三边关系可知当点P、C、B在一条直线上时，PC+PB有最小值，最后将点P的横坐标代入直线BC的解析式可求得点P的纵坐标；
（3）先判断出四边形PBQC时菱形时，点P是线段BC的垂直平分线，利用该特殊性建立方程求解．
解：（1）将B（4，0）代入y＝﹣x2+3x+m，
解得，m＝4，
二次函数解析式为y＝﹣x2+3x+4，
令x＝0，得y＝4，
∴C（0，4）；
（2）存在，如图所示
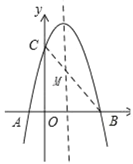
∵MC+MB≥BC，
∴当点M、C、B在一条直线上时，MC+MB有最小值．
∵点C的坐标为（0，4）．
设直线BC的解析式为y＝kx+4．
∵将点B、C的坐标代入得：
，解得k＝﹣1，b＝4，
∴直线BC的解析式为y＝﹣x+4，
∵抛物线的对称轴为
，
∴点M的横坐标为
，
∵将
代入直线BC的解析式得
，
∴点M的坐标为
；
（3）如图，
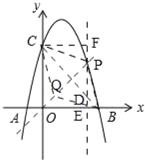
∵点P在抛物线上，
∴设P（m，﹣m2+3m+4），
当四边形PBQC是菱形时，点P在线段BC的垂直平分线上，
∵B（4，0），C（0，4）
∴线段BC的垂直平分线的解析式为y＝x，
∴m＝﹣m2+3m+4，
∴
，
∴
或
．
【题目】现实社会中，塑料袋仍然是白色污染的一部分，为了解塑料袋的使用情况，某校八年级环保小组随机抽取“幸福小区”40户居民家庭，记录了这些家庭某个月丢弃塑料袋的数量（单位：个）如下：
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据，解答以下问题：
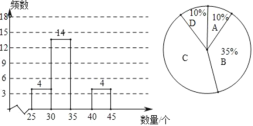
（1）若数据为x，按“组距为5”列出了如下的频数分布表，请将表中空缺的部分补充完整，并补全频数分布直方图；
分组 | 频数 |
A：25≤x＜30 | 4 |
B：30≤x＜35 | 14 |
C：35≤x＜40 | |
D：40≤x＜45 | 4 |
合计 | 40 |
（2）根据（1）中的直方图可以看出，这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多；（填分组序号）
（3）根据频数分布表，画出了如图所示的扇形统计图，请求出C组对应的扇形圆心角的度数；
（4）若该小区共有1000户居民家庭，请你估计每月丢弃的塑料袋数量不小于30个的家庭户数．
