题目内容
对任意两个正整数x、y，定义一个运算“★”为x★y=（x+2xy+y），若正整数a、b满足a★b=1154，则有序正整数对（a，b）共有分析：要求有序正整数对（a，b）共有几对，就要根据题中给出的运算，变形求出a或b的值，然后分析情况．求出有几对．
解答：解：由题意，得（a+2ab+b）=1154，
即2ab+a=1154-b
a（2b+1）=1154-b
a=
=
=-
+
=
（-1+
）
∴2a=-1+
11545=5×2309
10b+5=5无正整数解
10b+5=2309无正整数解
∴有序正整数对（a，b）共有0对．
故填0．
即2ab+a=1154-b
a（2b+1）=1154-b
a=
| 1154-b |
| 2b+1 |
-
| ||
| 2b+1 |
| 1 |
| 2 |
| 1154.5 |
| 2b+1 |
| 1 |
| 2 |
| 1154.5 | ||
b+
|
∴2a=-1+
| 11545 |
| 10b+5 |
11545=5×2309
10b+5=5无正整数解
10b+5=2309无正整数解
∴有序正整数对（a，b）共有0对．
故填0．
点评：此题考查二元一次方程的解法，可用整体代入的思想进行求解．
练习册系列答案
智慧小复习系列答案
相关题目
的三个正整数称为勾股数.
和
这三个数就是一组勾股数，请你验证这个结论.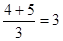 
；
；
；
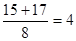，由此，某同学做出以下结论：在一组勾股数中，较大两个数的和能被最小的那个数整除.你认为他的结论正确吗？为什么？ 
的三个正整数称为勾股数.
和
这三个数就是一组勾股数，请你验证这个结论. 
；
；
；
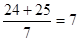，由此，某同学做出以下结论：在一组勾股数中，较大两个数的和能被最小的那个数整除.你认为他的结论正确吗？为什么？