题目内容
(2005•山西)在如图所示的图案中,黑白两色的直角三角形都全等.将它作为一个游戏盘,游戏规则是:按一定距离向盘中投镖一次,扎在黑色区域为甲胜,扎在白色区域为乙胜.你认为这个游戏公平吗?为什么?
【答案】分析:首先确定黑白两色三角形在整个圆中占的比例,根据这个比例即可求出黑白两色区域面积的概率,比较即可.
解答: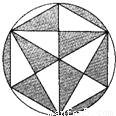 解:这个游戏是公平的.(1分)
解:这个游戏是公平的.(1分)
因为黑白两色的直角三角形都全等,且个数也分别相等.
所以黑白两色直角三角形面积的和也分别相等.(3分)
又因为黑白两色的弓形的弦长都是直角三角形都斜边,
所以黑白两色的弓形的面积和也分别相等.(6分)
因此黑白两色区域面积各占圆面积的50%,(7分)
即镖扎在黑白两色区域面积的概率均为50%,(8分)
故此游戏公平.(9分)
点评:本题将概率的求解设置于黑白两色的直角三角形的游戏中,考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=所求情况数与总情况数之比.
解答:
 解:这个游戏是公平的.(1分)
解:这个游戏是公平的.(1分)因为黑白两色的直角三角形都全等,且个数也分别相等.
所以黑白两色直角三角形面积的和也分别相等.(3分)
又因为黑白两色的弓形的弦长都是直角三角形都斜边,
所以黑白两色的弓形的面积和也分别相等.(6分)
因此黑白两色区域面积各占圆面积的50%,(7分)
即镖扎在黑白两色区域面积的概率均为50%,(8分)
故此游戏公平.(9分)
点评:本题将概率的求解设置于黑白两色的直角三角形的游戏中,考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 x与BC边相交于点D.
x与BC边相交于点D.