题目内容
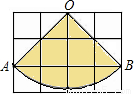
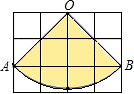如图，已知每个小正方形的边长为1cm，O、A、B都在小正方形顶点上，扇形OAB是某个圆锥的侧面展开图．
（1）计算这个圆锥侧面展开图的面积；
（2）求这个圆锥的底面半径．
解：（1）由图可知，OB=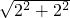
=2
；
则弧AB的长为=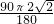
=π，
∴面积为：
×
×
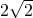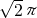=2π；
（2）设底面半径为r，
则2πr=π，
r=
．
这个圆锥的底面半径为cm．
分析：利用图形可以得到扇形的圆心角，和半径，利用扇形面积公式计算扇形的面积和底面半径即可．
点评：本题考查了圆锥的计算，解答本题需要准确掌握扇形的弧长公式，并且要善于读图．
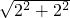=2；则弧AB的长为=
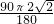=π，∴面积为：
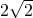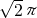××=2π；（2）设底面半径为r，
则2πr=
π，r=
．这个圆锥的底面半径为
cm．分析：利用图形可以得到扇形的圆心角，和半径，利用扇形面积公式计算扇形的面积和底面半径即可．
点评：本题考查了圆锥的计算，解答本题需要准确掌握扇形的弧长公式，并且要善于读图．
练习册系列答案
相关题目
如图，已知每个小正方形的边长为1cm，O、A、B都在小正方形顶点上，扇形OAB是某个圆锥的侧面展开图．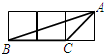
如图，已知每个小正方形的边长均为1，△ABC与△DEF的顶点都在小正方形的顶点上，那么△DEF与△ABC相似的是（ ）
