题目内容
(本小题满分12分)
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=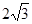 ,直线y=
,直线y=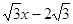 经过点C,交y轴于点G。
经过点C,交y轴于点G。
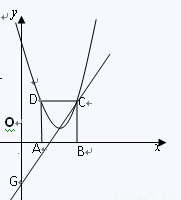
1.(1)点C、D的坐标分别是C( ),D( );
2.(2)求顶点在直线y=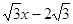 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
3.(3)将(2)中的抛物线沿直线y=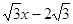 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。
【答案】
∴解析式为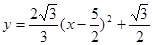
∴可设解析式为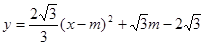
此时所求的解析式为: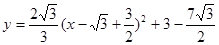 ;
;
此时所求的解析式为: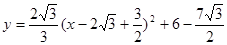 ;
;
1.(1)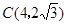
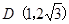
2.(2)由二次函数对称性得顶点横坐标为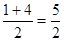 ,代入一次函数
,代入一次函数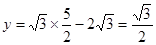 ,得顶点坐标为(
,得顶点坐标为(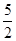 ,
,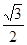 ),
),
∴设抛物线解析式为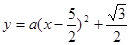 ,把点
,把点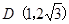 代入得,
代入得,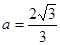
|
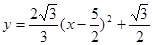
3.(3)设顶点E在直线上运动的横坐标为m,则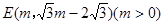
|
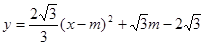
①当FG=EG时,FG=EG=2m,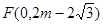 代入解析式得:
代入解析式得:
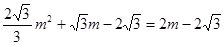 ,得m=0(舍去),
,得m=0(舍去),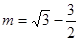 ,
,
|
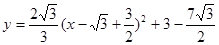 ;
;
②当GE=EF时,FG=4m,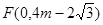 代入解析式得:
代入解析式得:
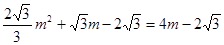 ,得m=0(舍去),
,得m=0(舍去),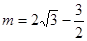 ,
,
|
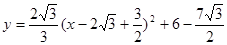 ;
;
③当FG=FE时,不存在;
【解析】略

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


