题目内容
13、若直线y=b(b为实数)与函数y=|x2-4x+3|的图象至少有三个公共点,则实数b的取值范围是
0<b≤1
.分析:先求x2-4x+3=0时x的值,再求x2-4x+3>0和x2-4x+3<0时,自变量的取值范围及对应的函数式,求函数式的取值范围,判断符合条件的b的值的范围.
解答:解:∵当x2-4x+3=0时,x=1或x=3,
∴当x<1或x>3时,x2-4x+3>0,即:y=x2-4x+3,函数值大于0,
当1<x<3时,x2-4x+3<0,即:y=-x2+4x-3,函数最大值为1,
故符合条件的实数b的取值范围是0<b≤1.
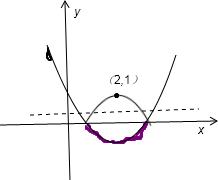
∴当x<1或x>3时,x2-4x+3>0,即:y=x2-4x+3,函数值大于0,
当1<x<3时,x2-4x+3<0,即:y=-x2+4x-3,函数最大值为1,
故符合条件的实数b的取值范围是0<b≤1.

点评:本题是分段函数的问题,按照绝对值里的数的符号,分段求函数,再求符合条件的b值范围.

练习册系列答案
相关题目
 直线y=
直线y= x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M.
x和y=-x+m,二次函数y=x2+px+q的图象的顶点为M. x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.
x与y=-x+m的交点处,试证明:无论m取何实数值,二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点. x上求异于M的点P,使点P在△CMA的外接圆上.
x上求异于M的点P,使点P在△CMA的外接圆上.