题目内容
平面内两条直线相交有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,…,若有20条直线相交,交点个数最多有( )个.
- A.380
- B.190
- C.400
- D.200
B
分析:画出图形,根据具体图形求出两条直线相交、三条直线相交、四条直线相交时的交点个数,总结出规律,即可计算出20条直线相交时的交点个数.
解答: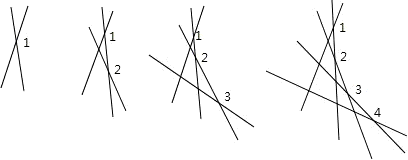 解:如图:2条直线相交有1个交点;
解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+…+n= 个交点;
个交点;
∴20条直线相交有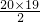 =190个交点.
=190个交点.
故选B.
点评:此题考查了直线相交的交点个数,体现了从一般到特殊再到一般的认知规律,有一定的挑战性,可以激发同学们的学习兴趣.
分析:画出图形,根据具体图形求出两条直线相交、三条直线相交、四条直线相交时的交点个数,总结出规律,即可计算出20条直线相交时的交点个数.
解答:
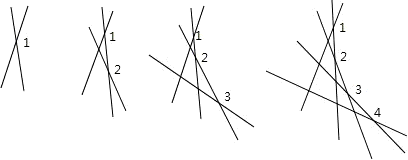 解:如图:2条直线相交有1个交点;
解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+…+n=
 个交点;
个交点;∴20条直线相交有
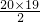 =190个交点.
=190个交点.故选B.
点评:此题考查了直线相交的交点个数,体现了从一般到特殊再到一般的认知规律,有一定的挑战性,可以激发同学们的学习兴趣.

练习册系列答案
相关题目
平面内两条直线相交有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,…,若有20条直线相交,交点个数最多有( )个.
| A、380 | B、190 | C、400 | D、200 |