题目内容
在平面直角坐标系xOy中，已知点A（2，-2），在坐标轴上确定一点B，使△AOB为等腰三角形，则符合条件的点B有 个．
考点：等腰三角形的判定,坐标与图形性质
专题：
分析：OA是等腰三角形的一边，确定第三点B，可以分OA是腰和底边两种情况进行讨论即可．
解答：8解：（1）若AO作为腰时，有两种情况，当A是顶角顶点时，B是以A为圆心，以OA为半径的圆与坐标轴的交点，共有2个（除O点）；
当O是顶角顶点时，B是以O为圆心，以OA为半径的圆与坐标轴的交点，有4个；
（2）若OA是底边时，B是OA的中垂线与坐标轴的交点，有2个．
以上8个交点没有重合的．故符合条件的点有8个．
故答案为：8．
当O是顶角顶点时，B是以O为圆心，以OA为半径的圆与坐标轴的交点，有4个；
（2）若OA是底边时，B是OA的中垂线与坐标轴的交点，有2个．
以上8个交点没有重合的．故符合条件的点有8个．
故答案为：8．
点评：本题考查了坐标与图形的性质和等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底，哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
练习册系列答案
阅读快车系列答案
相关题目
分别写有数字-l，-2，0，1，2的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到负数的概率是（ ）
A、
| ||
B、
| ||
C、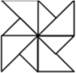
| ||
D、
|
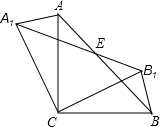如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α（0°＜α＜90°），得到△A1B1C，A1B1与AB相交于点ER，连接A1A，B1B，求证：△A1AE≌△BB1E．
如图，已知等腰△ABC的面积为16cm2，点D，E分别是AB，AC边的中点，则梯形DBCE的面为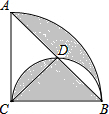
如图，△ABC是等腰直角三角形，在以BC为半径，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于D，若BC的长为2，则阴影部分的面积是下列各图中既是轴对称又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，已知三点A，B，C．读下列语句，用尺规作图：