题目内容
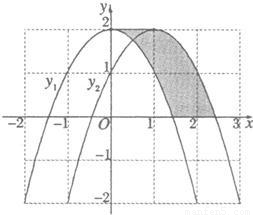
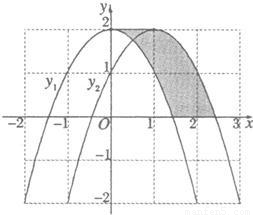
(2007•吉林)如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,回答下列问题:(1)抛物线y2的顶点坐标______;
(2)阴影部分的面积S=______;
(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,求抛物线y3的解析式.
【答案】分析:直接应用二次函数的知识解决问题.
解答:解:(1)读图找到最高点的坐标即可.故抛物线y2的顶点坐标为(1,2);(2分)
(2)把阴影部分进行平移,可得到阴影部分的面积即为图中两个方格的面积=1×2=2;(6分)
(3)由题意可得:抛物线y3的顶点与抛物线y2的顶点关于原点O成中心对称.
所以抛物线y3的顶点坐标为(-1,-2),于是可设抛物线y3的解析式为:
y=a(x+1)2-2.由对称性得a=1,
所以y3=(x+1)2-2.(10分)
点评:考查二次函数的相关知识,考查学生基础知识的同时还考查了识图能力.
解答:解:(1)读图找到最高点的坐标即可.故抛物线y2的顶点坐标为(1,2);(2分)
(2)把阴影部分进行平移,可得到阴影部分的面积即为图中两个方格的面积=1×2=2;(6分)
(3)由题意可得:抛物线y3的顶点与抛物线y2的顶点关于原点O成中心对称.
所以抛物线y3的顶点坐标为(-1,-2),于是可设抛物线y3的解析式为:
y=a(x+1)2-2.由对称性得a=1,
所以y3=(x+1)2-2.(10分)
点评:考查二次函数的相关知识,考查学生基础知识的同时还考查了识图能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目