题目内容
【题目】在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb﹣1，其中m，n为常数．
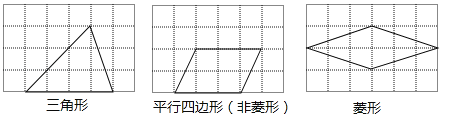
（1）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；
（2）利用（1）中的格点多边形确定m，n的值．
【答案】（1）作图见解析；（2）m=1，n=
【解析】试题分析：（1）利用格点图形的定义结合三角形以及平行四边形面积求法画图即可；
（2）利用已知图形和
得出关于m，n的关系式，进而求解即可．
试题解析：（1）如图所示：
；
（2）∵格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为：，其中m，n为常数，
∴三角形： 
，平行四边形： 
，菱形： 
，则
，解得：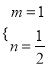 
．
练习册系列答案
相关题目
