题目内容
若实数a、b满足等式a2=7-3a，b2=7-3b，则代数式
+
之值为（ ）
| b |
| a |
| a |
| b |
A、-
| ||
B、
| ||
C、2或-
| ||
D、2或
|
分析：根据题意，分a=b和a≠b两种情况讨论，当a≠b时，易得a、b是方程x2=7-3x的根，利用根与系数的关系求解即可．
解答：解：当a=b时，
+
=2；
当a≠b时，
∵a、b是方程x2+3x-7=0的根，
∴a+b=-3，ab=-7，
∴
+
=
=
=
=-
；
综上所述，
+
=2或-
，
故选C．
| b |
| a |
| a |
| b |
当a≠b时，
∵a、b是方程x2+3x-7=0的根，
∴a+b=-3，ab=-7，
∴
| b |
| a |
| a |
| b |
| b2+a2 |
| ab |
| (a+b)2-2ab |
| ab |
| (-3)2+14 |
| -7 |
| 23 |
| 7 |
综上所述，
| b |
| a |
| a |
| b |
| 23 |
| 7 |
故选C．
点评：此题要注意分情况考虑，特别不要忘记a=b这种情况，同时也要利用根与系数的关系．
练习册系列答案
相关题目
若实数a、b满足等式a2=5-3a，b2=5-3b，则代数式
+
之值为（ ）
| b |
| a |
| a |
| b |
A、-
| ||
B、2或-
| ||
C、
| ||
D、2或
|
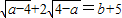，则代数式（a+b）+（a+b）3+（a+b）5+（a+b）7+…（a+b）2013的值是 ．