题目内容
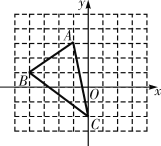
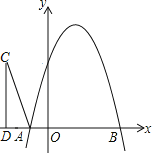
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点.
(1)求抛物线y=﹣x2+bx+c的解析式.
(2)在第二象限内取一点C,作CD⊥x轴于点D,连接AC,且AD=1,CD=5,将Rt△ACD沿x轴向右平移m个单位.
①当点C第一次落在抛物线上时,求m的值.
②当△ACD与抛物线y=﹣x2+bx+c的图象有交点时,求m的取值范围(直接答案即可)
【答案】(1)y=﹣x2+4x+5;(2)①m=2;②0≤m≤2或6≤m≤7.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)①根据自变量与函数值的对应关系,可得C点的横坐标,根据线段的和差,可得答案;
②根据图象第一次相交最初的交点是A,最终的交点是D点,根据自变量与函数值的对应关系,可得答案;根据图象第二次相交最初的交点是A,最终的交点是D点,根据自变量与函数值的对应关系,可得答案.
解:(1)将A,B点坐标代入函数解析式,得
![]() ,
,
解得![]() ,
,
抛物线的解析式为![]() ;
;
(2)①当y=5时,![]() ,解得
,解得![]() (不符合题意,舍),
(不符合题意,舍),
当点C第一次落在抛物线上时,C点的横坐标是0,
![]() 沿x轴向右平移
沿x轴向右平移![]() ,
,
m=2;
②![]() 与抛物线
与抛物线![]() 的图象第一次相交时的交点是由A到C,
的图象第一次相交时的交点是由A到C,
m=0时,交点是A,
C第一次在抛物线上,交点是C,此时![]() ,
,
![]() 与抛物线
与抛物线![]() 的图象第一次相交时,
的图象第一次相交时,![]() ;
;
![]() 与抛物线
与抛物线![]() 的图象第二次相交时最初的交点是C(或A),
的图象第二次相交时最初的交点是C(或A),
C第二次在抛物线上,交点是C,C点的坐标是![]() ,
,
此时![]() ;
;
第二次相交时最后的交点是D点,此时![]() ,
,
![]() 与抛物线
与抛物线![]() 的图象第二次相交时,
的图象第二次相交时,![]() .
.
综上所述:![]() 与抛物线
与抛物线![]() 的图象有交点时,m的取值范围是
的图象有交点时,m的取值范围是![]() 或
或![]() .
.

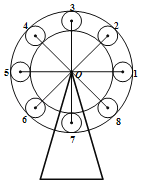
【题目】如图是一个摩天轮,它共有8个座舱,依次标为1~8号,摩天轮中心O的离地高度为50米,摩天轮中心到各座舱中心均相距25米,在运行过程中,当1号舱比3号舱高5米时,1号舱的离地高度为_____米.