题目内容
一个正方形的周长与一个等腰三角形的周长相等,若等腰三角形的两边长为 和
和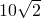 ,则这个正方形的对角线长为
,则这个正方形的对角线长为
- A.12
- B.

- C.2

- D.6

A
分析:根据题意分两种情况讨论:① 是底边和
是底边和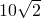 是腰;
是腰;
② 是腰和
是腰和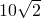 时底边两种情况讨论.当
时底边两种情况讨论.当 是底边和
是底边和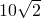 是腰时,等腰三角形的周长就可以求出,进而可知正方形的周长、边长,就可以求出对角线长.当
是腰时,等腰三角形的周长就可以求出,进而可知正方形的周长、边长,就可以求出对角线长.当 是腰和
是腰和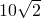 时,两边的和小于第三边,不能构成三角形,应舍去.
时,两边的和小于第三边,不能构成三角形,应舍去.
解答:①当 是腰和
是腰和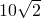 时,两边的和小于第三边,不能构成三角形,应舍去.
时,两边的和小于第三边,不能构成三角形,应舍去.
②当 是底边和
是底边和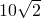 是腰时,
是腰时,
等腰三角形的周长是 ,因而可得正方形的边长是
,因而可得正方形的边长是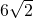 ,
,
故这个正方形的对角线长是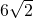 •cos45°=12;
•cos45°=12;
故选A.
点评:本题是一个已知等腰三角形的边长求周长问题,需要进行讨论,同时应该考虑到三角形的三边关系定理,这是解决这类问题容易忽视的一点.
分析:根据题意分两种情况讨论:①
 是底边和
是底边和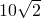 是腰;
是腰;②
 是腰和
是腰和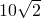 时底边两种情况讨论.当
时底边两种情况讨论.当 是底边和
是底边和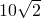 是腰时,等腰三角形的周长就可以求出,进而可知正方形的周长、边长,就可以求出对角线长.当
是腰时,等腰三角形的周长就可以求出,进而可知正方形的周长、边长,就可以求出对角线长.当 是腰和
是腰和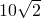 时,两边的和小于第三边,不能构成三角形,应舍去.
时,两边的和小于第三边,不能构成三角形,应舍去.解答:①当
 是腰和
是腰和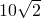 时,两边的和小于第三边,不能构成三角形,应舍去.
时,两边的和小于第三边,不能构成三角形,应舍去.②当
 是底边和
是底边和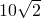 是腰时,
是腰时,等腰三角形的周长是
 ,因而可得正方形的边长是
,因而可得正方形的边长是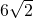 ,
,故这个正方形的对角线长是
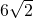 •cos45°=12;
•cos45°=12;故选A.
点评:本题是一个已知等腰三角形的边长求周长问题,需要进行讨论,同时应该考虑到三角形的三边关系定理,这是解决这类问题容易忽视的一点.

练习册系列答案
相关题目
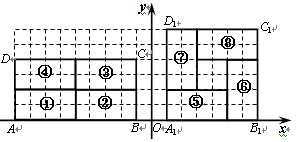
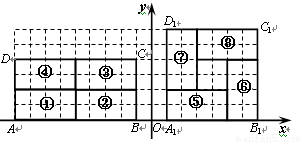
 23、(1)如图所示,在网格坐标系中,顶点在格点上的矩形ABCD被分割成四块全等的小矩形①,②,③,④,并经过一次或二次变换拼成正方形A1B1C1D1.试写出小矩形从①?⑤、③?⑦一种变换过程;
23、(1)如图所示,在网格坐标系中,顶点在格点上的矩形ABCD被分割成四块全等的小矩形①,②,③,④,并经过一次或二次变换拼成正方形A1B1C1D1.试写出小矩形从①?⑤、③?⑦一种变换过程;