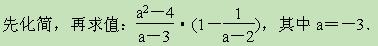题目内容
已知分式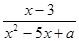 ,当
,当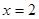 时,分式无意义,则
时,分式无意义,则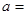 _______;当
_______;当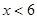 时,
时,
使分式无意义的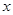 的值共有_______个
的值共有_______个
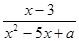 ,当
,当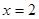 时,分式无意义,则
时,分式无意义,则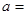 _______;当
_______;当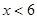 时,
时,使分式无意义的
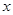 的值共有_______个
的值共有_______个6,2;
分析:根据分式无意义的条件:分母等于零求解.
解答:解:由题意,知当x=2时,分式无意义,
∴分母=x2-5x+a=22-5×2+a=-6+a=0,
∴a=6;
当x2-5x+a=0时,△=52-4a=25-4a,
∵a<6,
∴△=25-4a>0,
∴x2-5x+a=0有两个不相等的实数根,
对于每个符合题意的a,都有两个x的值使分式无意义,
∴a每确定一个值,对应的代数式的值就两个,
故当a<6时,使分式无意义的x的值共有2个.
故答案为6,2.
解答:解:由题意,知当x=2时,分式无意义,
∴分母=x2-5x+a=22-5×2+a=-6+a=0,
∴a=6;
当x2-5x+a=0时,△=52-4a=25-4a,
∵a<6,
∴△=25-4a>0,
∴x2-5x+a=0有两个不相等的实数根,
对于每个符合题意的a,都有两个x的值使分式无意义,
∴a每确定一个值,对应的代数式的值就两个,
故当a<6时,使分式无意义的x的值共有2个.
故答案为6,2.

练习册系列答案
相关题目
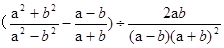 的值。
的值。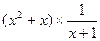 化简,再从-1,1两数中选取一
化简,再从-1,1两数中选取一 个适当的数作为x的
个适当的数作为x的 值代入求值.
值代入求值.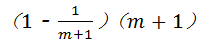 的结果是 .
的结果是 .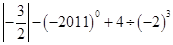 (2)
(2)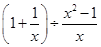
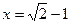 时,求代数式
时,求代数式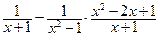 的值.
的值.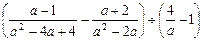 ,其中a=2-
,其中a=2-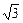

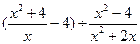 , 其中x="-3" 。
, 其中x="-3" 。