题目内容
请先阅读例题的解答过程,然后再解答:代数第三册在解方程3x(x+2)=5(x+2)时,先将方程变形为3x(x+2)-5(x+2)=0,这个方程左边可以分解成两个一次因式的积,所以方程变形为(x+2)(3x-5)=0.我们知道,如果两个因式的积等于0,那么这两个因式中至少有一个等于0;反过来,如果两个因式有一个等于0,它们的积等于0.因此,解方程(x+2)(3x-5)=0,就相当于解方程x+2=0或3x-5=0,得到原方程的解为x1=-2,x2=
| 5 |
| 3 |
根据上面解一元二次方程的过程,王力推测:a﹒b>0,则有
|
|
| 5x-1 |
| 2x-3 |
分析:先根据利用因式分解法求方程根的方法判断出王力的推测是正确的,再根据其范例及不等式的性质列出不等式组,求出其解集即可.
解答:解:王力的推测是正确的.
∴
>0
∴
(1)
或
(2)
解不等式组(1)得:x>
;
解不等式组(2)得:x<
;
∴不等式
>0的解集是x>
或x<
.
∴
| 5x-1 |
| 2x-3 |
∴
|
或
|
解不等式组(1)得:x>
| 3 |
| 2 |
解不等式组(2)得:x<
| 1 |
| 5 |
∴不等式
| 5x-1 |
| 2x-3 |
| 3 |
| 2 |
| 1 |
| 5 |
点评:此题是一道材料分析题,考查了同学们的阅读理解能力.对于分是不等式,应当根据“两数相除,同号得正”进行分析.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 .
.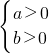 或
或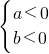 ,请判断王力的推测是否正确?若正确,请你求出不等式
,请判断王力的推测是否正确?若正确,请你求出不等式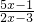 >0的解集,如果不正确,请说明理由.
>0的解集,如果不正确,请说明理由. .
.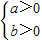 或
或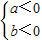 ,请判断王力的推测是否正确?若正确,请你求出不等式
,请判断王力的推测是否正确?若正确,请你求出不等式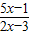 >0的解集,如果不正确,请说明理由.
>0的解集,如果不正确,请说明理由. .
. 或
或 ,请判断王力的推测是否正确?若正确,请你求出不等式
,请判断王力的推测是否正确?若正确,请你求出不等式 >0的解集,如果不正确,请说明理由.
>0的解集,如果不正确,请说明理由.