Question

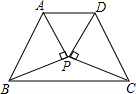将等腰Rt△APB绕直角顶点P按顺时针方向旋转130°之后，得Rt△CPD后，四边形ABCD是等腰梯形吗？

Answer 1

解：四边形ABCD是等腰梯形，
理由是：∵将等腰Rt△APB绕直角顶点P按顺时针方向旋转130°之后，得Rt△CPD，
∴∠APC=130°，AB=CD，AP=PD，BP=CP，∠APB=∠DPC=90°，
∴∠BPD=130°，
∴∠PAD=∠PDA=（180°-∠APD）=70°，∠PBC=∠PCB=（180°-∠BPC）=20°，
∵△APB是等腰直角三角形，
∴∠APB=90°，AP=BP，
∴∠PAB=∠PBA=45°，
∴∠DAB+∠ABC=70°+45°+45°+20°=180°，
∴AD∥BC，
∴四边形ABCD是梯形，
∵AB=CD，
∴梯形ABCD是等腰梯形．
分析：根据旋转得出∠APC=130°，AB=CD，AP=PD，BP=CP，∠APB=∠DPC=90°，分别求出∠APD、∠PAD、∠PBC的度数，求出∠PAB=∠PBA=45°，求出∠DAB+∠ABC=180°，推出AD∥BC即可．
点评：本题考查了三角形的内角和定理，等腰三角形性质，等腰梯形的判定的应用，主要考查学生运用定理进行推理的能力，题目具有一定的代表性，是一道比较好的题目．