题目内容
(2012•银海区一模)有一抛物线桥拱,水面AB宽20米,当水面上升3米后水面CD宽10米,此时因降暴雨洪水以平均每小时0.25米 的速度上升,再通过几小时,洪水将会淹到拱桥顶?
的速度上升,再通过几小时,洪水将会淹到拱桥顶?
 的速度上升,再通过几小时,洪水将会淹到拱桥顶?
的速度上升,再通过几小时,洪水将会淹到拱桥顶?分析:先以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,设此抛物线的解析式是y=ax2,再将点D的坐标(5,y0),点B的坐标(10,y0-3)代入y=ax2,得到关于a,y0的二元一次方程组,解方程组得出y0=-1,即拱桥顶O到CD的距离为1,然后根据时间=路程÷速度即可求解.
解答: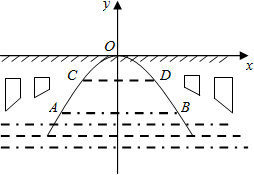 解:如图所示,以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,
解:如图所示,以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,
设此抛物线的解析式是y=ax2,则点D的坐标是(5,y0),点B的坐标是(10,y0-3),
由题意,得
,
解得
.
∵y0=-1,
∴拱桥顶O到CD的距离为1,
1÷0.25=4(小时).
答:再通过4小时,洪水将会淹到拱桥顶.
 解:如图所示,以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,
解:如图所示,以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,设此抛物线的解析式是y=ax2,则点D的坐标是(5,y0),点B的坐标是(10,y0-3),
由题意,得
|
解得
|
∵y0=-1,
∴拱桥顶O到CD的距离为1,
1÷0.25=4(小时).
答:再通过4小时,洪水将会淹到拱桥顶.
点评:本题考查二次函数的实际应用,难度适中,建立适当的平面直角坐标系,求出点D的纵坐标是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 按顺时针方向旋转90°后的图形是( )
按顺时针方向旋转90°后的图形是( )



 按顺时针方向旋转90°后的图形是( )
按顺时针方向旋转90°后的图形是( )


