Question

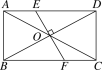
【题目】如图，矩形ABCD的对角线AC与BD交于点O，过点O作BD的垂线分别交AD，BC于E，F两点．若AC＝2，∠DAO＝30°，则FC的长度为(　　)

A. 1B. 2

C. D.

Answer 1

【答案】A

【解析】

由矩形的性质可得OA=OB=OC=OD=AC=，∠ABC=90°，即可得∠ADO=∠DAO=∠OBC=∠ACB＝30°，在Rt△ABC中求得 BC=3；在Rt△BOF中，求得BF=2，所以CF=BC-BF=1.

∵四边形ABCD是矩形，AC＝2，

∴OA=OB=OC=OD=AC=，∠ABC=90°，

∴∠ADO=∠DAO=∠OBC=∠ACB＝30°，

在Rt△ABC中，AC＝2，∠ACB＝30°，

∴BC=3；

∵EF⊥BD，

∴∠BOF=90°，

在Rt△BOF中，OB=，∠OBC=30°，

∴BF=2，

∴CF=BC-BF=1，

故选A．