Question

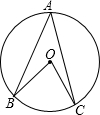如图，在⊙O中，AB、AC是弦，O在∠BAC的内部，则∠BOC、∠B、∠C三个角之间的等量关系是________．

Answer 1

∠BOC=2（∠B+∠C）
分析：根据等腰三角形的性质推出∠B=∠BAO，∠C=∠CAO，根据圆周角定理得出∠BOC=2∠BAC，代入即可求出答案．
解答：
连接OA，
∵OA=OB，OA=OC，
∴∠B=∠BAO，∠C=∠CAO，
∵弧BC对的圆周角是∠BAC，对的圆心角是∠BOC，
∴∠BOC=2∠BAC，
∵∠BAC=∠BAO+∠CAO=∠B+∠C，
∴∠BOC=2（∠B+∠C），
故答案为：∠BOC=2（∠B+∠C），
点评：本题考查了等腰三角形的性质和圆周角定理，注意：一条弧所对的圆周角等于它所对的圆心角的一半．