题目内容
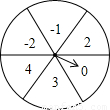
如图是一个被平均分成6等份的转盘，每一个扇形中都标有相应的数字，甲乙两人分别转动转盘，设甲转动转盘后指针所指区域内的数字为x，乙转动转盘后指针所指区域内的数字为y（当指针在边界上时，重转一次，直到指向一个区域为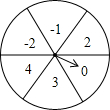
止）．（1）直接写出甲转动转盘后所指区域内的数字为负数的概率；
（2）用树状图或列表法，求出点（x，y）落在第二象限内的概率．
分析：（1）根据古典概率的知识，利用概率公式即可求得答案；
（2）根据题意列出表格，然后根据表格即可求得所有等可能的结果与点（x，y）落在第二象限内的情况，然后利用概率公式求解即可求得答案．
（2）根据题意列出表格，然后根据表格即可求得所有等可能的结果与点（x，y）落在第二象限内的情况，然后利用概率公式求解即可求得答案．
解答：解：（1）∵一共有6种等可能的结果，甲转动转盘后所指区域内的数字为负数的有：-1，-2共2种情况，
∴甲转动转盘后所指区域内的数字为负数的概率为：
=
；
（2）根据题意，列表得：
∴点（x，y）的坐标一共有36种等可能的结果，且每种结果发生的可能性相等，其中点（x，y）落在第二象限的结果共有6种，
∴点（x，y）落在第二象限内的概率为：
=
．
∴甲转动转盘后所指区域内的数字为负数的概率为：
| 2 |
| 6 |
| 1 |
| 3 |
| 甲 乙 |
-1 | -2 | 0 | 2 | 3 | 4 |
| -1 | （-1，-1） | （-2，-1） | （0，-1） | （2，-1） | （3，-1） | （4，-1） |
| -2 | （-1，-2） | （-2，-2） | （0，-2） | （2，-2） | （3，-2） | （4，-2） |
| 0 | （-1，0） | （-2，0） | （0，0） | （2，0） | （3，0） | （4，0） |
| 2 | （-1，2） | （-2，2） | （0，2） | （2，2） | （3，2） | （4，2） |
| 3 | （-1，3） | （-2，3） | （0，3） | （2，3） | （3，3） | （4，3） |
| 4 | （-1，4） | （-2，4） | （0，4） | （2，4） | （3，4） | （4，4） |
∴点（x，y）的坐标一共有36种等可能的结果，且每种结果发生的可能性相等，其中点（x，y）落在第二象限的结果共有6种，
∴点（x，y）落在第二象限内的概率为：
| 6 |
| 36 |
| 1 |
| 6 |
点评：此题考查了树状图法与列表法求概率．此题难度不大，解题的关键是根据题意画出树状图或列出表格，注意树状图法与列表法可以不重不漏的表示出所有等可能的结果，注意用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
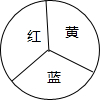今年“五一”节，某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被平均分成3份）．规定：顾客每购买100元的商品，就能获得连续转动转盘2次的机会．转盘停止后，如果2次转盘的指针都对着红色区域，那么顾客可以获得50元购物券；如果只有1次转盘的指针对着红色区域，那么顾客可以获得15元购物券；如果顾客不愿意转转盘，那么可以直接获得购物券10元（如果指针停在等分线上，那么重转1次，直到指针指向某一扇形内）．
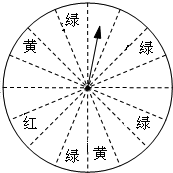某商场举行开业酬宾答谢活动，设立了一个可以自由转动的转盘（如图，转盘被平均分成16份），并规定：顾客每购买88元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得50元、30元、20元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券10元．
止）．