Question

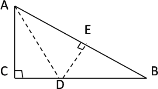
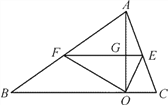
【题目】如图，等腰△ABC中，BA＝BC，AO⊥BC于点O，AO＝3CO＝6．F是AB边上的一个动点，过F作FE∥BC交AC边于点E，交AO于点G，连结FO，EO，设EF长为x，△EFO的面积为S．

(1)求OB的长；

(2)求S关于x的函数表达式和x的取值范围；

(3)判断：当△EFO的面积最大时，△EFO和△CBA是否相似并说明理由．

Answer 1

【答案】(1)8;(2) (0＜x＜10) ;(3)见解析.

【解析】

（1）由AO=3CO=6易得CO=2，结合AB=BC可得AB=BC=BO+2，这样在Rt△ABO中由AB2=AO2+BO2可得（2+OB）2=62+OB2，由此即可解得OB的值；

（2）由EF∥BC可得△AFE∽△ABC，由此可得，结合AG=AO-GO，EF=x及（1）中所得结论即可用含x的式子表达GO的长，再利用S△OEF=EF·GO即可求得所求函数关系式了；

（3）由（2）中所得解析配方可求得当△OEF面积最大时，EF=5，由此可知此时EF：BC=1：2，由EF∥BC可得△AFE∽△ABC，从而可得，由此可得点E、F是AC、AB的中点，结合AO⊥BC可得OF=AB，OE=AC，从而可得，由此即可得到△EFO∽△CBA.

(1)∵AO＝3CO＝6，

∴CO＝2，

∴AB =BC= BO+2，

∵AO⊥BC，

∴AB2＝AO2＋OB2，

∴(2＋OB)2＝36＋OB2，

解得OB＝8；

(2) 由(1)得BC=OB+2=10，

∵FE∥BC，

∴△AFE∽△ABC，

∴，即 ，

解得：OG=，

∴S＝EF×OG＝，

即(0＜x＜10) ；

(3) 当△EFO的面积最大时，△EFO∽△CBA，理由如下：

∵ ，

∴当x=5，即EF=5时，S最大= ，

此时：，

∵FE∥BC，

∴△AFE∽△ABC，

∴，

∴E，F分别是AC，AB的中点，

∵AO⊥BC，

∴，，

∴，

∴△EFO∽△CBA.