ЬтФПФкШн
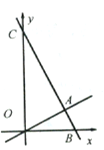
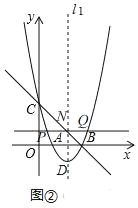
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љx+3ЗжБ№гыxжсЁЂyНЛгкЕуBЁЂCЃЛХзЮяЯпy=x2+bx+cОЙ§ЕуBЁЂCЃЌгыxжсЕФСэвЛИіНЛЕуЮЊЕуAЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌЖдГЦжсЮЊl1ЃЌЖЅЕуЮЊDЃЎ
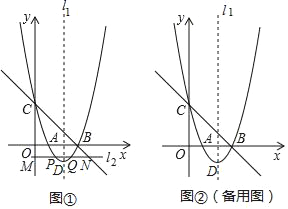
ЃЈ1ЃЉЧѓХзЮяЯпy=x2+bx+cЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЕуMЃЈ0ЃЌmЃЉЮЊyжсЩЯвЛЖЏЕуЃЌЙ§ЕуMзїжБЯпl2ЦНаагкxжсЃЌгыХзЮяЯпНЛгкЕуPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉЃЌгыжБЯпBCНЛгкЕуNЃЈx3ЃЌy3ЃЉЃЌЧвx2ЃОx1ЃО0ЃЎ
ЂйНсКЯКЏЪ§ЕФЭМЯѓЃЌЧѓx3ЕФШЁжЕЗЖЮЇЃЛ
ЂкШєШ§ИіЕуPЁЂQЁЂNжаЧЁКУгавЛЕуЪЧЦфЫћСНЕуЫљСЌЯпЖЮЕФжаЕуЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x2Љ4x+3ЃЛЃЈ2ЃЉЂй0ЃМx3ЃМ4ЃЌЂкmЕФжЕЮЊ![]() Лђ1ЃЎ
Лђ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжБЯпy=Љx+3ЗжБ№гыxжсЁЂyНЛгкЕуBЁЂCЧѓЕУЕуBЁЂCЕФзјБъЃЌдйДњШыy=x2+bx+cЧѓЕУbЁЂcЕФжЕЃЌМДПЩЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЂйЯШЧѓЕУХзЮяЯпЕФЖЅЕузјБъЮЊDЃЈ2ЃЌЉ1ЃЉЃЌЕБжБЯпl2ОЙ§ЕуDЪБЧѓЕУm=Љ1ЃЛЕБжБЯпl2ОЙ§ЕуCЪБЧѓЕУm=3ЃЌдйгЩx2ЃОx1ЃО0ЃЌПЩЕУЉ1ЃМy3ЃМ3ЃЌМДПЩЉ1ЃМЉx3+3ЃМ3ЃЌЫљвд0ЃМx3ЃМ4ЃЛЂкЗжЕБжБЯпl2дкxжсЕФЯТЗНЪБЃЌЕуQдкЕуPЁЂNжЎМфКЭЕБжБЯпl2дкxжсЕФЩЯЗНЪБЃЌЕуNдкЕуPЁЂQжЎМфСНжжЧщПіЧѓmЕФжЕМДПЩ.
ЃЈ1ЃЉдкy=Љx+3жаЃЌСюx=0ЃЌдђy=3ЃЛ
Сюy=0ЃЌдђx=3ЃЛЕУBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЌ
НЋЕуBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЕФзјБъДњШыy=x2+bx+c
ЕУЃК![]() ЃЌНтЕУ
ЃЌНтЕУ ![]()
Ёрy=x2Љ4x+3ЃЛ
ЃЈ2ЃЉЁпжБЯпl2ЦНаагкxжсЃЌ
Ёрy1=y2=y3=mЃЌ
ЂйШчЭМЂйЃЌy=x2Љ4x+3=ЃЈxЉ2ЃЉ2Љ1ЃЌ
ЁрЖЅЕуЮЊDЃЈ2ЃЌЉ1ЃЉЃЌ
ЕБжБЯпl2ОЙ§ЕуDЪБЃЌm=Љ1ЃЛ
ЕБжБЯпl2ОЙ§ЕуCЪБЃЌm=3
Ёпx2ЃОx1ЃО0ЃЌ
ЁрЉ1ЃМy3ЃМ3ЃЌ
МДЉ1ЃМЉx3+3ЃМ3ЃЌ
ЕУ0ЃМx3ЃМ4ЃЌ
ЂкШчЭМЂйЃЌЕБжБЯпl2дкxжсЕФЯТЗНЪБЃЌЕуQдкЕуPЁЂNжЎМфЃЌ
ШєШ§ИіЕуPЁЂQЁЂNжаЧЁКУгавЛЕуЪЧЦфЫћСНЕуЫљСЌЯпЖЮЕФжаЕуЃЌдђЕУPQ=QNЃЎ
Ёпx2ЃОx1ЃО0ЃЌ
Ёрx3Љx2=x2Љx1ЃЌ
МД x3=2x2Љx1ЃЌ
Ёпl2ЁЮxжсЃЌМДPQЁЮxжсЃЌ
ЁрЕуPЁЂQЙигкХзЮяЯпЕФЖдГЦжсl1ЖдГЦЃЌ
гжХзЮяЯпЕФЖдГЦжсl1ЮЊx=2ЃЌ
Ёр2Љx1=x2Љ2ЃЌ
МДx1=4Љx2ЃЌ
Ёрx3=3x2Љ4ЃЌ
НЋЕуQЃЈx2ЃЌy2ЃЉЕФзјБъДњШыy=x2Љ4x+3
ЕУy2=x22Љ4x2+3ЃЌгжy2=y3=Љx3+3
Ёрx22Љ4x2+3=Љx3+3ЃЌ
Ёрx22Љ4x2=ЉЃЈ3x2Љ4ЃЉ
МД x22Љx2Љ4=0ЃЌНтЕУx2=![]() ЃЌЃЈИКжЕвбЩсШЅЃЉЃЌ
ЃЌЃЈИКжЕвбЩсШЅЃЉЃЌ
Ёрm=ЃЈ![]() ЃЉ2Љ4ЁС
ЃЉ2Љ4ЁС![]() +3=
+3=![]()
ШчЭМЂкЃЌЕБжБЯпl2дкxжсЕФЩЯЗНЪБЃЌЕуNдкЕуPЁЂQжЎМфЃЌ
ШєШ§ИіЕуPЁЂQЁЂNжаЧЁКУгавЛЕуЪЧЦфЫћСНЕуЫљСЌЯпЖЮЕФжаЕуЃЌдђЕУPN=NQЃЎ
гЩЩЯПЩЕУЕуPЁЂQЙигкжБЯпl1ЖдГЦЃЌ
ЁрЕуNдкХзЮяЯпЕФЖдГЦжсl1ЃКx=2ЃЌ
гжЕуNдкжБЯпy=Љx+3ЩЯЃЌ
Ёрy3=Љ2+3=1ЃЌМДm=1ЃЎ
ЙЪmЕФжЕЮЊ![]() Лђ1ЃЎ
Лђ1ЃЎ

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ