题目内容
某人骑自行车由甲地驶向乙地,如果每小时比原来的速度快6公里,便可以早到5分钟;如果每小时比原来的速度慢5公里,便要迟到6分钟.则甲、乙两地的距离为________公里.
15
分析:设此人正常的速度为x,行走的时间为y,则根据如果每小时比原来的速度快6公里,便可以早到5分钟;如果每小时比原来的速度慢5公里,便要迟到6分钟列出关于x、y的方程组,求得x、y的值即可求解.
解答:设此人正常的速度为x,行走的时间为y,
则由题意知:(x+6)(y-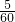 )=xy,
)=xy,
(x-5)(y+ )=xy,
)=xy,
化简得x-5-50y=0;
x+6-72y=0,
解得x=30,y=0.5,
甲乙两地的距离为xy=15公里.
答:甲乙两地的距离为15公里.
点评:本题考查了二元一次方程组的应用,本题中列出关于x、y的方程组并且求x、y的值是解题的关键.
分析:设此人正常的速度为x,行走的时间为y,则根据如果每小时比原来的速度快6公里,便可以早到5分钟;如果每小时比原来的速度慢5公里,便要迟到6分钟列出关于x、y的方程组,求得x、y的值即可求解.
解答:设此人正常的速度为x,行走的时间为y,
则由题意知:(x+6)(y-
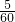 )=xy,
)=xy,(x-5)(y+
 )=xy,
)=xy,化简得x-5-50y=0;
x+6-72y=0,
解得x=30,y=0.5,
甲乙两地的距离为xy=15公里.
答:甲乙两地的距离为15公里.
点评:本题考查了二元一次方程组的应用,本题中列出关于x、y的方程组并且求x、y的值是解题的关键.

练习册系列答案
相关题目