Question

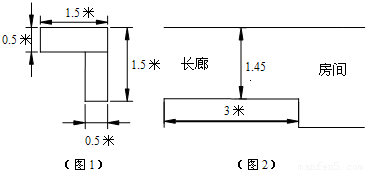
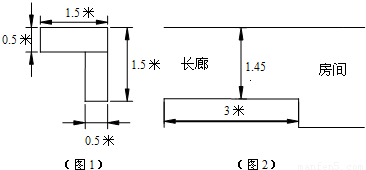
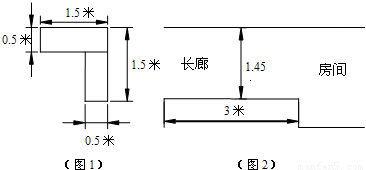
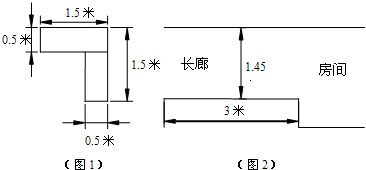如图1所示的是某立式家具（角书橱）的横断面，请你设计一个方案（角书橱高2m，房间高2.6m，所以不必从高度方面考虑方案的设计），按此方案，可使该家具能通过如图2中的长廊搬入房间．把你设计的方案画成草图，并说明按此方案可把家具搬入房间的理由．（注：搬运过程中不准拆家具，不准损坏墙壁）

Answer 1

分析：只要DH的长在1.45米以内，即可顺利通过，构造直角三角形，利用相应的三角函数求得DH长，看是否在1.45米以内即可．

解答：解：方案如图（1）所示．
理由：如图（2），连接AB，延长DC交BA延长线于点E．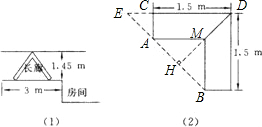
由题意知，AM=BM，
∴△ACE是等腰直角三角形．
∴CE=0.5，DE=DC+CE=2．
作DH⊥AB于点H，
则DH=DE•sin∠HED=2×sin45°=

2

．
∵

2

＜1.45，
∴可按方案设计图将家具搬入房间．

点评：解本题的关键是把实际问题转化为数学问题，只要把它抽象到解直角三角形中即可求出．
用到的知识点为：点到直线的所有连线中，垂线段最短．