题目内容
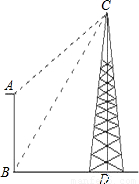
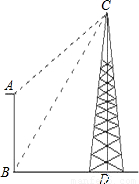
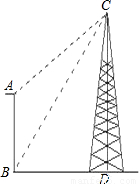
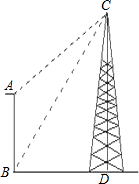 瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势高低相同.求塔高CD.
瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势高低相同.求塔高CD.
解:设塔高CD为x,则BD= x,
x,
由BD•tan60°-BD•tan45°=AB,BD= x代入,
x代入,
得:x- x=20,解得:x=30+10
x=20,解得:x=30+10 .
.
答:塔高CD为(30+10 )米.
)米.
分析:可先由CD及仰角60°的正切值表示BD,再由BD及两仰角的正切值可表示出AB,即BD•tan60°-BD•tan45°=AB,求得CD.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
 x,
x,由BD•tan60°-BD•tan45°=AB,BD=
 x代入,
x代入,得:x-
 x=20,解得:x=30+10
x=20,解得:x=30+10 .
.答:塔高CD为(30+10
 )米.
)米.分析:可先由CD及仰角60°的正切值表示BD,再由BD及两仰角的正切值可表示出AB,即BD•tan60°-BD•tan45°=AB,求得CD.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
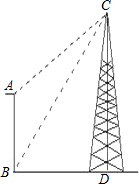 瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势高低相同.求塔高CD.
瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势高低相同.求塔高CD.