题目内容
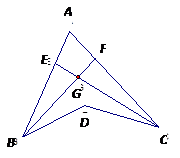
 如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )
如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )分析:根据三角形内角和定理可求得∠DBC+∠DCB的度数,再根据三角形内角和定理及三角形角平分线的定义可求得∠ABC+∠ACB的度数,从而不难求得∠A的度数.
解答: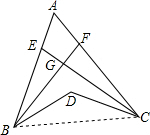 解:连接BC.
解:连接BC.
∵∠BDC=130°,
∴∠DBC+∠DCB=180°-130°=50°,
∵∠BGC=100°,
∴∠GBC+∠GCB=180°-100°=80°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=
∠ABD+
∠ACD=30°,
∴∠ABC+∠ACB=110°,
∴∠A=180°-110°=70°.
故选B.
 解:连接BC.
解:连接BC.∵∠BDC=130°,
∴∠DBC+∠DCB=180°-130°=50°,
∵∠BGC=100°,
∴∠GBC+∠GCB=180°-100°=80°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC+∠ACB=110°,
∴∠A=180°-110°=70°.
故选B.
点评:本题考查的是三角形内角和定理,根据题意作出辅助线,构造出三角形是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
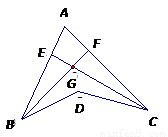
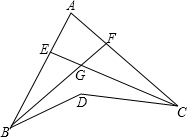 如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BE与CE交于G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )| A、50° | B、55° | C、70° | D、80° |