题目内容
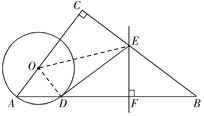
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

【答案】(1)直线DE与⊙O相切;(2)4.75.
【解析】试题分析:(1) 直线DE与⊙O相切,连接OD,根据等腰三角形的性质可得∠A=∠ODA,根据线段垂直平分线的性质及等腰三角形的性质易得∠B=∠EDB,易证ODA+∠EDB=![]() ,即可得∠ODE=
,即可得∠ODE=![]() -
-![]() =
=![]() ,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =
,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,即
,即![]() ,解得x的值即可得线段DE的长.
,解得x的值即可得线段DE的长.
试题解析: (1) 直线DE与⊙O相切.
理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA.
∵EF是BD的垂直平分线,
∴EB="ED."
∴∠B=∠EDB.
∵∠C=![]() ,
,
∴∠A+∠B=![]() .
.
∴∠ODA+∠EDB=![]() .
.
∴∠ODE=![]() -
-![]() =
=![]() .
.
∴直线DE与⊙O相切.
(2) 解法一:
连接OE,
设DE=x,则EB=ED=x,CE=8-x.
∵∠C=∠ODE =![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
即DE=![]() .
.
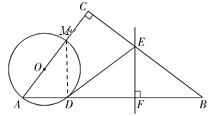
解法二:
连接DM,
∵AM是直径,
∴∠MDA=![]() ,AM=4.
,AM=4.
又∵∠C=![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() , ∴AD=2.4.
, ∴AD=2.4.
∴BD=10-2.4=7.6.
∴BF=![]() .
.
∵EF⊥BD,∠C=![]() ,
,
∴![]() .
.
∴![]() , BE=
, BE=![]() .
.
∴DE=![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目