题目内容
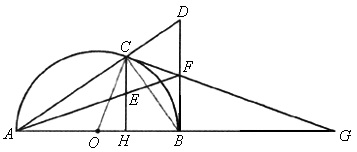
(2006,盐城非课改)已知:如图,C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连结AE并延长,交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.

答案:略
解析:
解析:
|
(1) 证明:∵CH⊥AB,DB⊥AB,∴△AEH∽△AFB,△ACE∽△ADF,∴ 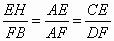 ∵HE=EC,∴BF=FD. ∵HE=EC,∴BF=FD.
(2) 证明:如图,连结CB、OC.∵ AB是直径,∴∠ACB=90°,∵F是BD中点,∴∠ BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO.∴∠ OCF=90°,∴CG是⊙O的切线.(3) 解:由FC=FB=FE得∠FCE=∠FEC,可证得 FA=FG、且AB=BC.由切割线定理得 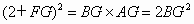 .① .①
在 Rt△BGF中,由勾股定理得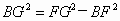 .② .②
由①、②得 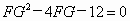 , ,
解之得 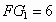 , ,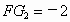 (舍去), (舍去),
∴ 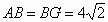 , ,
∴⊙ O的半径为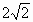 . .
|

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
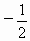
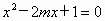 的一个解,则m的值是
的一个解,则m的值是