Question

在一个布口袋中装着只有颜色不同，其他都相同的白、红、黑三种颜色的小球各1只，甲、乙两人进行模球游戏：甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．如果规定：乙摸到与甲相同颜色的球为乙胜，否则为输，则乙在游戏中能获胜的概率为（　　）

• A、

  1

  3

• B、

  1

  4

• C、

  1

  9

• D、

  2

  3

Answer 1

分析：先画出树形图，即可得到共有9种可能，其中乙摸到与甲相同颜色的球有3种可能，再根据概率的含义即可得到乙在游戏中能获胜的概率．

解答：解：根据题意有：

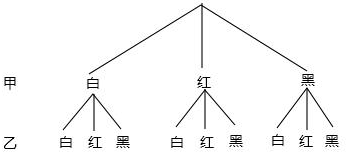
共有9种可能，其中乙摸到与甲相同颜色的球有3种可能，
所以乙在游戏中能获胜的概率=

3

9

=

1

3

．
故选A．

点评：本题考查了利用树形图求事件的概率．