题目内容
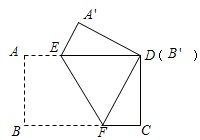
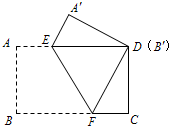 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则DF=________cm,重叠部分△DEF的面积是________cm2.
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则DF=________cm,重叠部分△DEF的面积是________cm2.
3.4 5.1
分析:根据折叠的性质知:AE=A′E,AB=A′D;可设AE为x,用x表示出A′E和DE的长,进而在Rt△A′DE中求出x的值,即可得到A′E的长;再根据△EA′D≌△FCD,可以得出DF=DE,继而求出DF的长;并且可求出△A′ED和梯形A′EFD的面积,两者的面积差即为所求的△DEF的面积.
解答:设AE=A′E=x,则DE=5-x;
在Rt△A′ED中,A′E=x,A′D=AB=3cm,ED=AD-AE=5-x;
由勾股定理得:x2+9=(5-x)2,
解得x=1.6,
即AE=A′E=AE=1.6cm,ED=3.4cm;
∵∠A′DF=∠EDC=90°,
∴∠A′DE=∠CDF,
又A′D=CD,∠EA′D=∠FCD,
∴△EA′D≌△FCD,
∴A′E=CF,故BF=ED=3.4cm;
∴S△DEF=S梯形A′DFE-S△A′DE= (A′E+DF)•DF-
(A′E+DF)•DF- A′E•A′D,
A′E•A′D,
= ×(5-x+x)×3-
×(5-x+x)×3- ×x×3,
×x×3,
= ×5×3-
×5×3- ×1.6×3,
×1.6×3,
=5.1(cm2).
故答案为:3.4,5.1.
点评:此题考查了图形的折叠变换,能够根据折叠的性质和勾股定理求出AE、A′E的长是解答此题的关键.
分析:根据折叠的性质知:AE=A′E,AB=A′D;可设AE为x,用x表示出A′E和DE的长,进而在Rt△A′DE中求出x的值,即可得到A′E的长;再根据△EA′D≌△FCD,可以得出DF=DE,继而求出DF的长;并且可求出△A′ED和梯形A′EFD的面积,两者的面积差即为所求的△DEF的面积.
解答:设AE=A′E=x,则DE=5-x;
在Rt△A′ED中,A′E=x,A′D=AB=3cm,ED=AD-AE=5-x;
由勾股定理得:x2+9=(5-x)2,
解得x=1.6,
即AE=A′E=AE=1.6cm,ED=3.4cm;
∵∠A′DF=∠EDC=90°,
∴∠A′DE=∠CDF,
又A′D=CD,∠EA′D=∠FCD,
∴△EA′D≌△FCD,
∴A′E=CF,故BF=ED=3.4cm;
∴S△DEF=S梯形A′DFE-S△A′DE=
 (A′E+DF)•DF-
(A′E+DF)•DF- A′E•A′D,
A′E•A′D,=
 ×(5-x+x)×3-
×(5-x+x)×3- ×x×3,
×x×3,=
 ×5×3-
×5×3- ×1.6×3,
×1.6×3,=5.1(cm2).
故答案为:3.4,5.1.
点评:此题考查了图形的折叠变换,能够根据折叠的性质和勾股定理求出AE、A′E的长是解答此题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
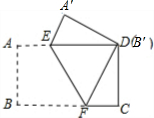 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积是( )
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积是( )| A、7.5cm2 | B、5.1cm2 | C、5.2cm2 | D、7.2cm2 |
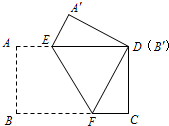 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则DF=
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则DF=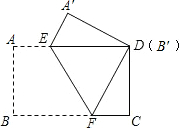 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积是
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积是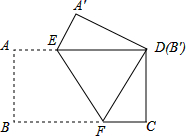 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,求重叠部分△DEF的面积.
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,求重叠部分△DEF的面积.