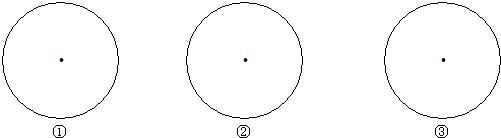
题目内容
不过圆心的直线l交⊙O于C、D两点,AB是⊙O的直径,AE⊥l于E,BF⊥l于F.(1)如图,在下面三个圆中分别补画出满足上述条件的具有不同位置关系的图形;
(2)请你观察(1)中所画的图形,写出一个各图都具有的两条线段相等的结论(不再标注其它字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程);
(3)请你选择(1)中的一个图形,证明(2)所得出的结论.
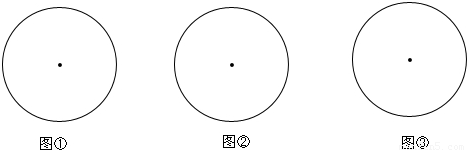
【答案】分析:(1)考查你的画图能力和思维能力,这里要渗透发散思维,要分情况而论;
(2)利用平行线的性质即可找出EC=FD;
(3)利用垂径定理即可证明.
解答:解:(1)如下图所示.
(2)EC=FD和ED=FC.
证明:①EC=FD.
根据垂径定理,CH=DH,
根据中位线定理,EH=FH,
所以EH-CH=FH-DH,
故EC=DF.
②ED=FC.
因为ED=EF+DF,
FC=EF+EC,
由①可得,
EC=DF,
所以ED=FC.

(3)以①图为例来证明.
过O作OH⊥l于H,
∵AE⊥l,BF⊥l,
∴AE∥OH∥BF,
又∵OA=OB,
∴EH=HF,再由垂径定理可得CH=DH,
∴EH-CH=FH-DH,
即EC=FD.
以②图为例来证明.
过O作OH⊥l于H,
∵AE⊥l,BF⊥l,
∴AE∥OH∥BF,
又∵OA=OB,
∴EH=HF(一组平行在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等),再由垂径定理可得CH=DH,
∴EH-CH=FH-DH,
即EC=FD.
点评:本题综合考查了学生的几何知识,做几何题画图是关键,所以学生一定要养成画图的习惯.
(2)利用平行线的性质即可找出EC=FD;
(3)利用垂径定理即可证明.
解答:解:(1)如下图所示.
(2)EC=FD和ED=FC.
证明:①EC=FD.
根据垂径定理,CH=DH,
根据中位线定理,EH=FH,
所以EH-CH=FH-DH,
故EC=DF.
②ED=FC.
因为ED=EF+DF,
FC=EF+EC,
由①可得,
EC=DF,
所以ED=FC.

(3)以①图为例来证明.
过O作OH⊥l于H,
∵AE⊥l,BF⊥l,
∴AE∥OH∥BF,
又∵OA=OB,
∴EH=HF,再由垂径定理可得CH=DH,
∴EH-CH=FH-DH,
即EC=FD.
以②图为例来证明.
过O作OH⊥l于H,
∵AE⊥l,BF⊥l,
∴AE∥OH∥BF,
又∵OA=OB,
∴EH=HF(一组平行在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等),再由垂径定理可得CH=DH,
∴EH-CH=FH-DH,
即EC=FD.
点评:本题综合考查了学生的几何知识,做几何题画图是关键,所以学生一定要养成画图的习惯.

练习册系列答案
相关题目