题目内容
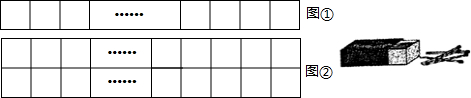
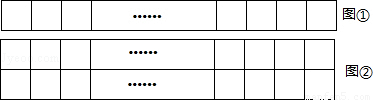
现用a根长度相同的火柴棒,按如图①摆放时可摆成m个正方形,按如图②摆放时可摆成2n个正方形.

(1)如图①,当m=3时,a=
如图②,当m=2时,a=
(2)当a=37时,若按图①摆放可以摆出了几个正方形?若按图②摆放可以摆出了几个正方形?
(3)现有2013根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状.请你直接写出一种摆放方法,并通过计算验证你的结论.

(1)如图①,当m=3时,a=
10
10
;如图②,当m=2时,a=
12
12
;(2)当a=37时,若按图①摆放可以摆出了几个正方形?若按图②摆放可以摆出了几个正方形?
(3)现有2013根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状.请你直接写出一种摆放方法,并通过计算验证你的结论.
分析:(1)根据每多一个正方形多用2根火柴棒写出摆放m个正方形所用的火柴棒的根数,然后把m=3代入进行计算即可得解;
根据每多2个正方形多用5根火柴棒写出摆放2n个小正方形所用的火柴棒的根数,然后把m=2代入进行计算即可得解;
(2)根据a相等列出关于m、n的关系式;
(3)可以摆出图①说明a是比3的倍数多1的数,可以摆出图②说明2a是比5的倍数多2的数,所以,2a取5与6的倍数大2的数,并且现有2013根火柴棒进而得出答案.
根据每多2个正方形多用5根火柴棒写出摆放2n个小正方形所用的火柴棒的根数,然后把m=2代入进行计算即可得解;
(2)根据a相等列出关于m、n的关系式;
(3)可以摆出图①说明a是比3的倍数多1的数,可以摆出图②说明2a是比5的倍数多2的数,所以,2a取5与6的倍数大2的数,并且现有2013根火柴棒进而得出答案.
解答:解:(1)由图可知,图①每多1个正方形,多用3根火柴棒,所以,m个小正方形共用3m+1根火柴棒,
图②每多2个正方形,多用5根火柴棒,所以,2n个小正方形共用5n+2根火柴棒,
当m=3时,a=3×3+1=10,
图②可以摆放2×5=12个小正方形;
故答案为:10,12;
(2)当a=37时,
3m+1=37,
解得:m=12,
5n+2=37,
解得;n=7,
按图①摆放可以摆出了12个正方形,
若按图②摆放可以摆出14个正方形;
(3)∵3m+1+5n+2=2013,
∴3m+5n=2010,
当m=10,n=396,是方程的根,
∴第一个图形摆放3×10+1=31根火柴棒,
第二个图形摆放5×396+2=1982根火柴棒,
∵31+1982=2013,
∴符合题意(答案不唯一).
图②每多2个正方形,多用5根火柴棒,所以,2n个小正方形共用5n+2根火柴棒,
当m=3时,a=3×3+1=10,
图②可以摆放2×5=12个小正方形;
故答案为:10,12;
(2)当a=37时,
3m+1=37,
解得:m=12,
5n+2=37,
解得;n=7,
按图①摆放可以摆出了12个正方形,
若按图②摆放可以摆出14个正方形;
(3)∵3m+1+5n+2=2013,
∴3m+5n=2010,
当m=10,n=396,是方程的根,
∴第一个图形摆放3×10+1=31根火柴棒,
第二个图形摆放5×396+2=1982根火柴棒,
∵31+1982=2013,
∴符合题意(答案不唯一).
点评:本题是对图形变化规律的考查,观察出正方形的个数与火柴棒的根数之间的变化关系是解题的关键.

练习册系列答案
相关题目